三角形の五心の覚えておくべき性質を整理 レベル ★ 最難関大受験対策 平面図形 更新日時 三角形の五心の定義と重要な性質をまとめました。 三角形の五心は有名で豊かな性質を持っており,数学オリンピックの初等幾何の証明問題では超頻出接線と弦のつくる角の定理の証明 では、なぜこのような定理が成り立つのか。 簡単に確認しておきましょう! なぜ、次のような位置にある角の大きさが等しくなるのでしょうか。 これを考えるには、まず 接点から、直径になるように線を引いて 下の内接円といい、中心を内心といいます。 下の「定理8」は三角形の3つの角の二等分線は1点で交わること の証明ですが、その証明方法をはじめてみる方にとっては、「へぇ~ 垂線か」と思われるかもしれませんが、「角の二等分線」が「各辺から の距離
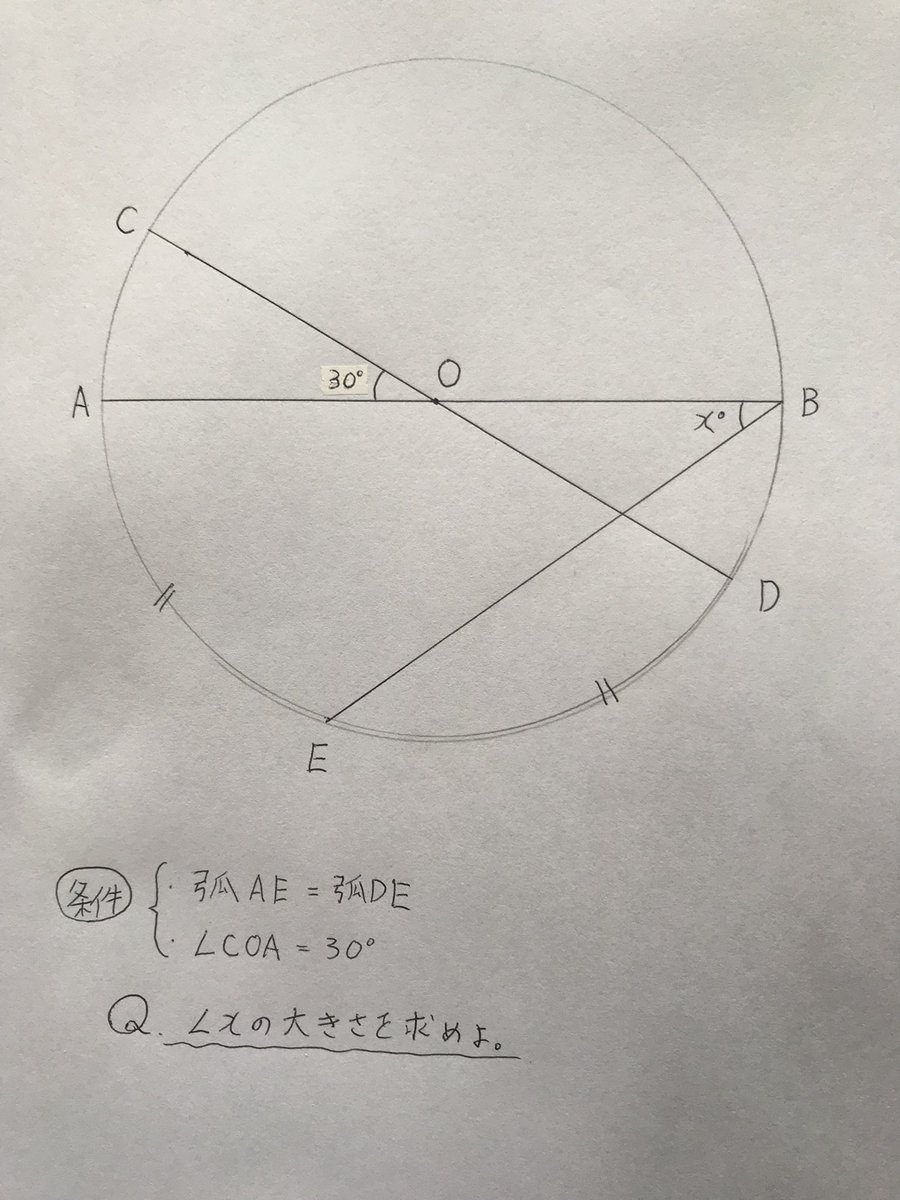
円の性質
円の性質 角度
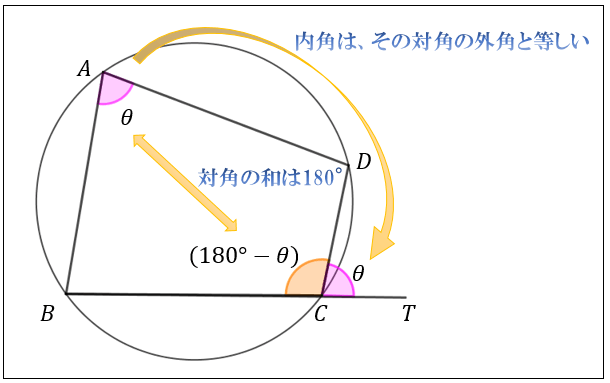
円の性質 角度-三角形の内心 ・ 外心 ・ 重心 三角形の3つの内角の2等分線は、1点で交わり、その点から3辺までの距離は等しい。 この1点で交わった点 I を三角形の内心という。 半径 IL の円が三角形の内接円である。 高校数学A図形の性質円に内接する四角形まとめと問題 円に内接する四角形に関するまとめと問題です。 円に内接する四角形の角を求める問題、四角形の角から円に内接するかを判断する問題、トレミーの定理についても簡単に触れています。 1 円に




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく
円・扇形の公式まとめ 円周: 2πr 2 π r 円の面積: πr2 π r 2 扇形の弧の長さ: 2πr× a 360 2 π r × a 360 扇形の面積: πr2 × a 360 π r 2 × a 360 扇形の面積(弧の長さ l l からの導出): 1 2lr 1 2 l r ※半径: r r 、円周率: π π 、中心角: a a 、扇形の弧の長さ DR リード 円の性質円周角の角度の求め方の3つのパターン 円周角の角度の求め方は3パターン?? やあ,Drリードだぞいっ!☆角度・距離などキーワードを拾い 上げる。 ・a~d から見たゴールの写真を提示 する ☆角度とはどこの角度か?など共通 で理解が必要な事柄を確認する。 関心・意欲・態度 しっかりと予測できて いるか(ワークシート) 6 円の性質を使っ て、問題に
外接円の半径の公式 公式①正弦定理から求める 公式②3 辺と面積から求める 外接円の半径の求め方例題 外接円の性質 性質①外心(外接円の中心)と垂直二等分線 性質②外心と各頂点との距離 外接円の書き方 外接円の練習問題重要な図形の一つに円があります。 ここでは円の基本的な用語である中心角、弧、弦などの定義を解説します。 そして、これらの性質についての解説も行います。 円とは はじめに円の定義から始めます。 円とは、ある点との距離が等しくなる点の集合で小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題
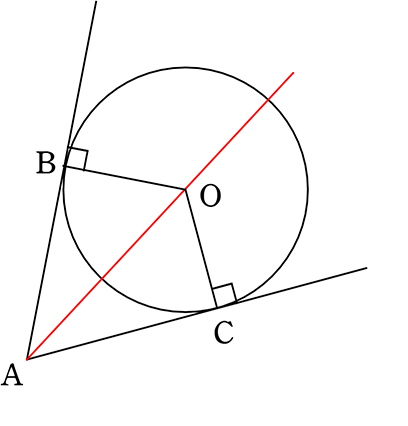
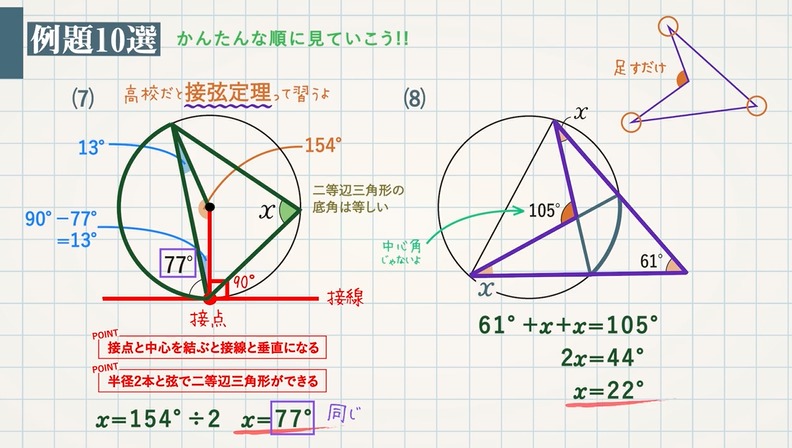
接弦定理4 円周角の定理 (入試問題) → 携帯版は別頁 弧(こ)・弦(げん)とは 円周の一部を「弧」という. 例 右図の赤で示した部分を 弧 AB などという.(これに対して灰色で示した線分は 弦 AB という.) ※ 1つの弦により円周全体は2つの弧に 外心では、外接円という円を扱います。 つまり、円の性質も合わせて知っておく必要があるということです。 また三角形と円が絡む話題として、他に外心と内心があります。 併せて確認しておいてください! ※三角形の内心 定義と性質を証明問題形式で これこそが、図形問題なのである。 測ったらタルトが本当に45度で切られていて見事だった 肩慣らしとして、これを解いてみよう。 出題は、「xの角度を求めよ」。 三角形の内角の和は180度。 かつタルトは二等辺三角形なので、角ABCは (180度45度)/2 = 675
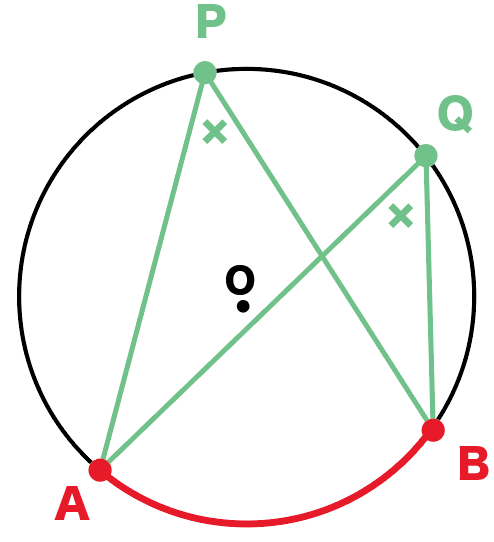



3分でわかる 円周角の定理とはなんだろう Qikeru 学びを楽しくわかりやすく
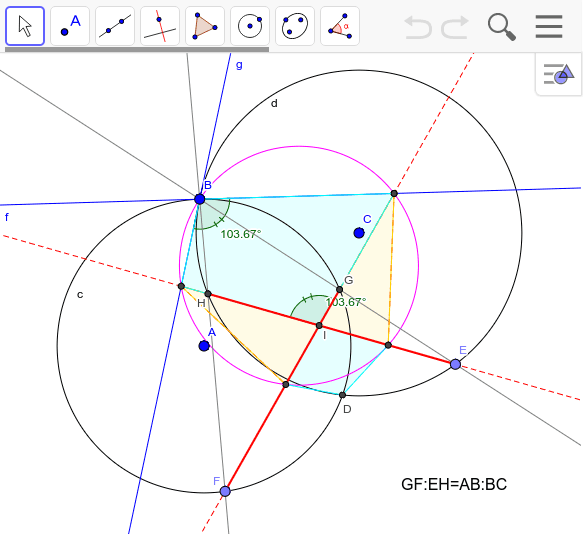



交わる二つの円に関する性質 Geogebra
最後に外心、内心、重心のポイントをまとめておきましょう。 外心 3辺の垂直二等分線が交わる点 各頂点から等しい距離にある 各頂点から線を結ぶと二等辺三角形ができるので、底角が等しい 円周角の定理が使える 内心 3つの角の二等分線が 内接円の性質 内接円には、大きく \(2\) つの性質があります。 性質①内心と各辺の距離 多角形のそれぞれの辺が内接円の接線となっていて、各接点から引いた垂線の交点が内接円の中心(内心)となります。イ 多角形の角の性質 多角形の内角の総和 四角形の内角の総和は、「360°」ですね! では、なぜ360°なのでしょうか? それは、「四角形が三角形2つからできている」からですね! 三角形2つからできているのがわかりますね そして、角度マークを



1




角度を求めよう 円とブーメラン 中学数学 Wiki Atwiki アットウィキ
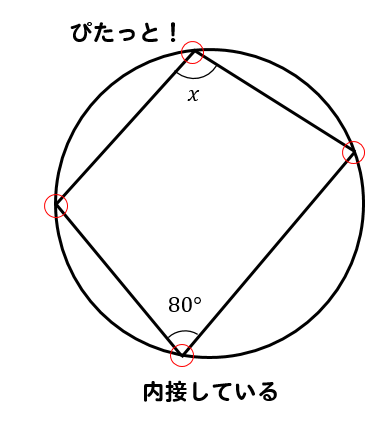
円の半径r=300でのn=8の多角形の1辺の長さaはではなくて?ではないでしょうか。 keisanより r=300の時、辺の長さがとなるのは、 円に外接する正多角形と考円周角は中心角の半分(中心角は円周角の2倍)だから x=2× (31°17°)=96° (答)円に内接する四角形の角度 円に内接する四角形の対角の和は 180° である。 → a c = 180°, b d = 180°
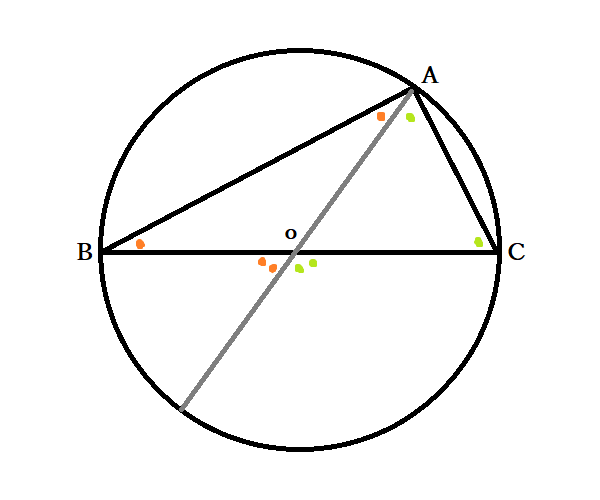



中3数学 円周角の定理とは 円周角と中心角の関係の証明法 円の性質の応用問題 中学 Curlpingの幸せblog



円周角の定理とは 定理の逆や証明 問題の解き方 受験辞典
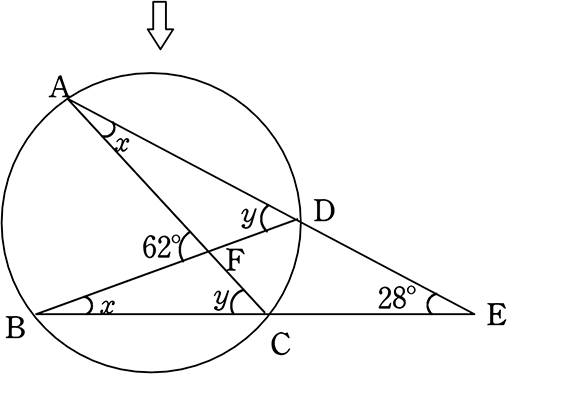
数学Aの円で使う定理・性質の一覧 円周角の定理 弧ABに対する円周角の大きさはつねに一定であり、その角の大きさは、その弧に対する中心角の大きさの半分である。 ・∠ACB=∠ADB ・∠AOB=2∠ACB=2∠ADB また、次の図のよ 三角関数の必ず覚えなくてはならない5つの性質 ①sin2θcos2θ=1 ② ①、②とも三角関数の定義の単位円を思い出せば、簡単です。 ①は単位円の方程式がX 2 Y 2 =1だから、それにX=cosθ、Y=sinθを代入すれば出来ます。 また、②は だからX=cosθ、Y=sinθを代入 「円に内接する四角形の性質」ではありませんが,円周上に4点がある場合方べきの定理を使うことが多いです。 性質4 (方べきの定理) AE\times EC=BE\times ED AE × EC = BE ×E D
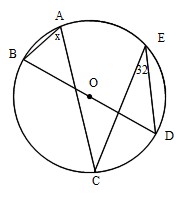



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット
以上、円に関する性質でした! これらの「武器」と次の過程で学ぶ「三平方の定理」があれば 中学数学の円に関する問題で解けないものはないですね! お疲れ様でした! その他の問題は、「問題集」で !!MathAquarium練習問題図形の性質 14 14 次の図において,x の値を求めよ。ただし,(3)の直線PT は接点をT とする円の接線である。 (1) (2) (3) Px A 9 D C 5 P B8 6 A D 4 C B x 3 2 P A T B x 円の性質 っていう単元 を勉強していくよ。 今日は、この単元でいちばん大事な、 円周角の定理とはなにか?? をまとめてみたんだ。 計算や証明で使ったりするから、しっかりおさえてあげてね。 = もくじ = 円周角・中心角とは?? 円周角の定理とは?




円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく
・直角三角形(斜辺と角度) 直角三角形の斜辺と角度から、底辺と高さと面積を計算します。 三角関数 ・角度から三角関数 角度(度またはラジアン)から三角関数を計算します。 ・三角関数から角度(逆三角関数) 三角関数から角度(逆三角関数)を計算します。 この図でaの角度は何度になるか求めなさい。 解説 基本事項でもお伝えしたように三角定規は下の図のように角度が決まっています。 問題の図でbは45°、cは30°なので、三角形の内角は180°である性質を利用すると、aの角度は、 180°(45°30°)=105° 外接円の存在 任意の三角形には三頂点を通る円が存在する。 三頂点を通る円を 外接円 という。 ABC A B C の辺 AB A B の中点を M AB M A B とし、 辺 BC B C の中点を M BC M B C とする。 また、 辺 AB A B と辺 BC B C の垂直二等分線の交点を O O とする。 このとき
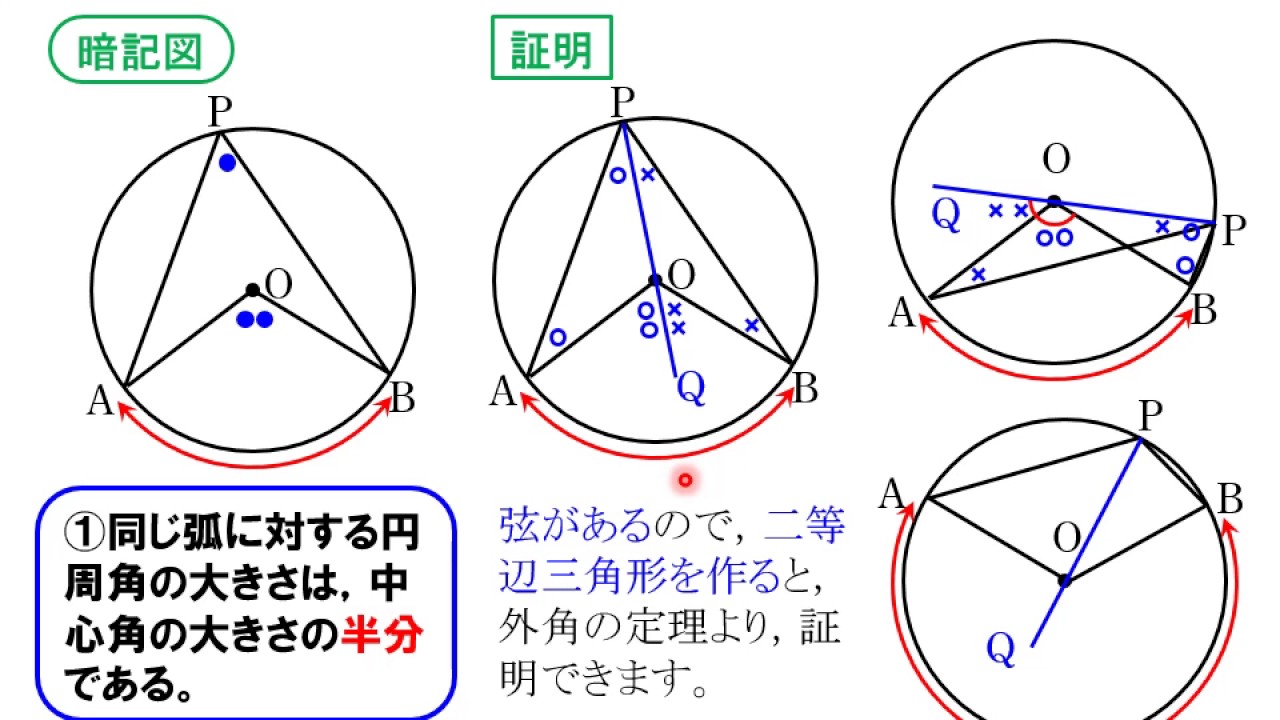



円と角度02 円周角の性質 Youtube




円周角の定理はこれで完璧 定理の証明と様々な問題の解法
Bunryu Kamimura 二つの円の交わる角度を変えてみる。 円の交点の角度=交線の角度という関係がある。 さらに、元の長さは半径が同じなら等しい。 円に内接する四角形の性質まとめ対角の和が180°になる理由 Tooda Yuuto 18年8月22日 / 19年9月9日 四角形の つの頂点 がすべて同じ円周上にある(内側から接している)とき、「四角形 は円に内接する」といいます。 反対に、四角形 の つの辺がすべて→ ページの先頭に戻る ④ その他余談
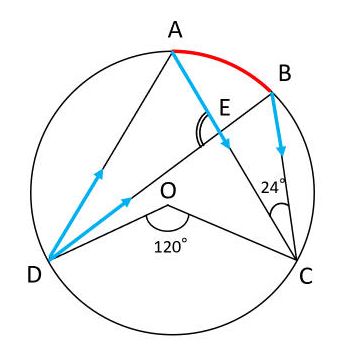



円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア
外接円、外心について 「外接円」や「外心」の用語や意味は中学の 教科書の発展内容としてあります。 それぞれの各辺の垂直二等分線は一点でまじわり、その点Dを中心に円を書くと Dを中心に三角形の3つの頂点を通る円を書くことができて、この円整数の性質 例題(11) 練習問題 練習問題+解答図形の性質 例題(18) 練習問題 練習問題+解答 三角形の角の二等分線と比 メネラウスの定理,チェバの定理 円周角の定理(円に内接する四角形の性質) 接弦定理 方べきの定理 三垂線の定理数 学 ii 式と




6本の缶を最短の紐で束ねる意外な方法とは 円と球の不思議な雑学 横山 明日希 ブルーバックス 講談社 1 4
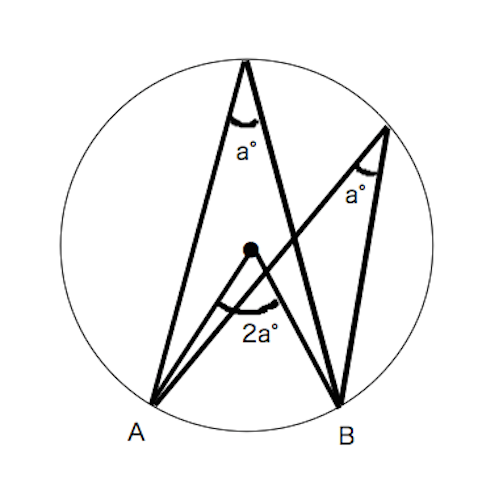



円周角の定理 苦手な数学を簡単に




円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ
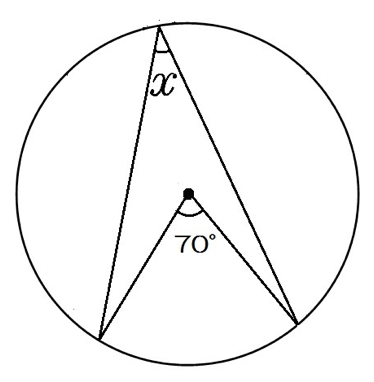



円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




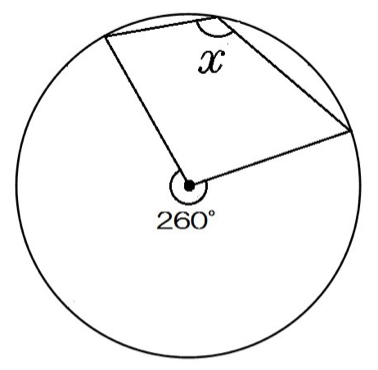
円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者
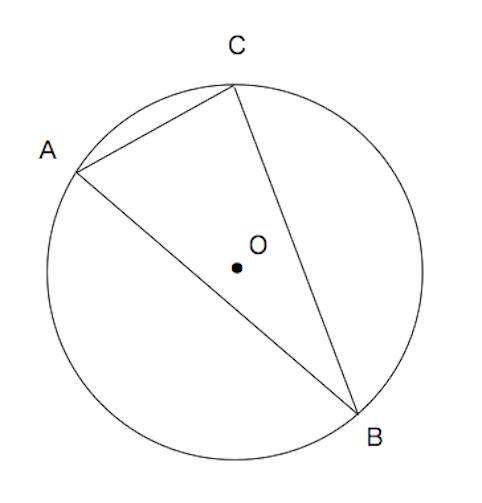



円周角の定理 練習問題 角度がわからない 苦手な数学を簡単に




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生
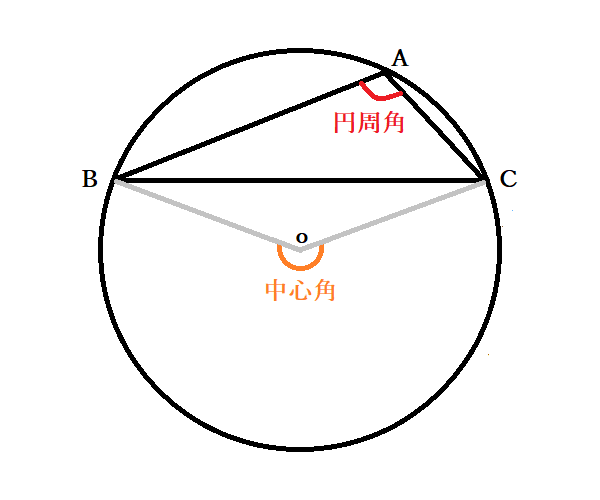



中3数学 円周角の定理とは 円周角と中心角の関係の証明法 円の性質の応用問題 中学 Curlpingの幸せblog



中学数学 円周角 中心角




円と角度のチェックテスト2 円周角を求める発展問題 難しい問題もあります Youtube



円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく



円周角




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者




中学数学 円周角 中心角




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ




接弦定理とは何か 角度別に分かるその証明方法 アタリマエ




円と接線の性質を利用して図形の角度を求める問題 バカでもわかる 中学数学




中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく



円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者



円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ
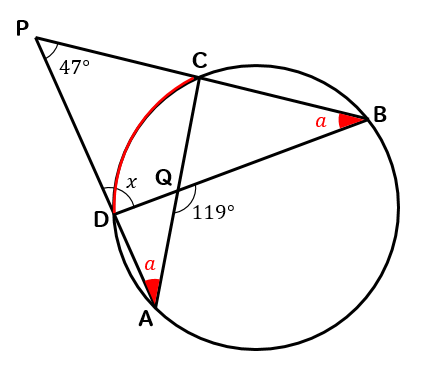



円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ




高校数学a 共円条件 4点が同一円周上にある条件 受験の月




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




中学数学 円周角 中心角




円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学
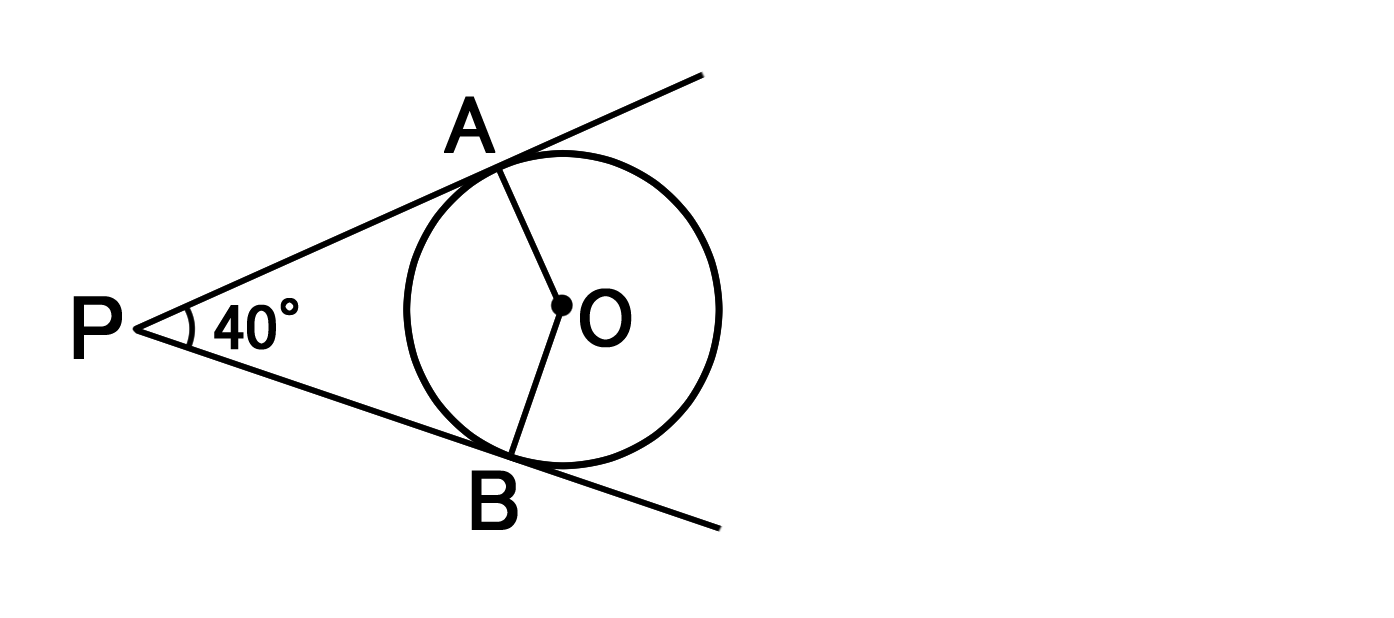



円と接線の性質を利用して図形の角度を求める問題 バカでもわかる 中学数学



円周角




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく
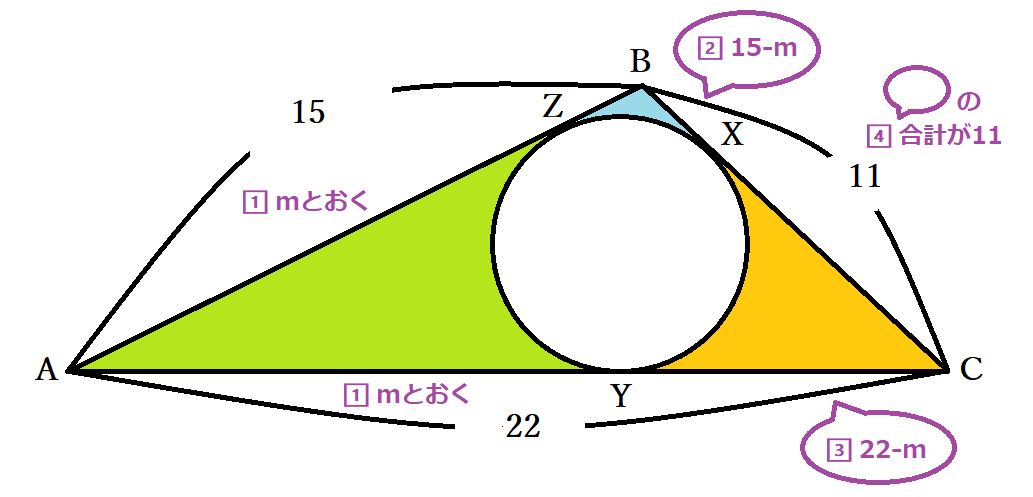



円の接線の性質 公式 円外の点pを通る円oの接線の長さが等しいことの証明 中学数学 Curlpingの幸せblog
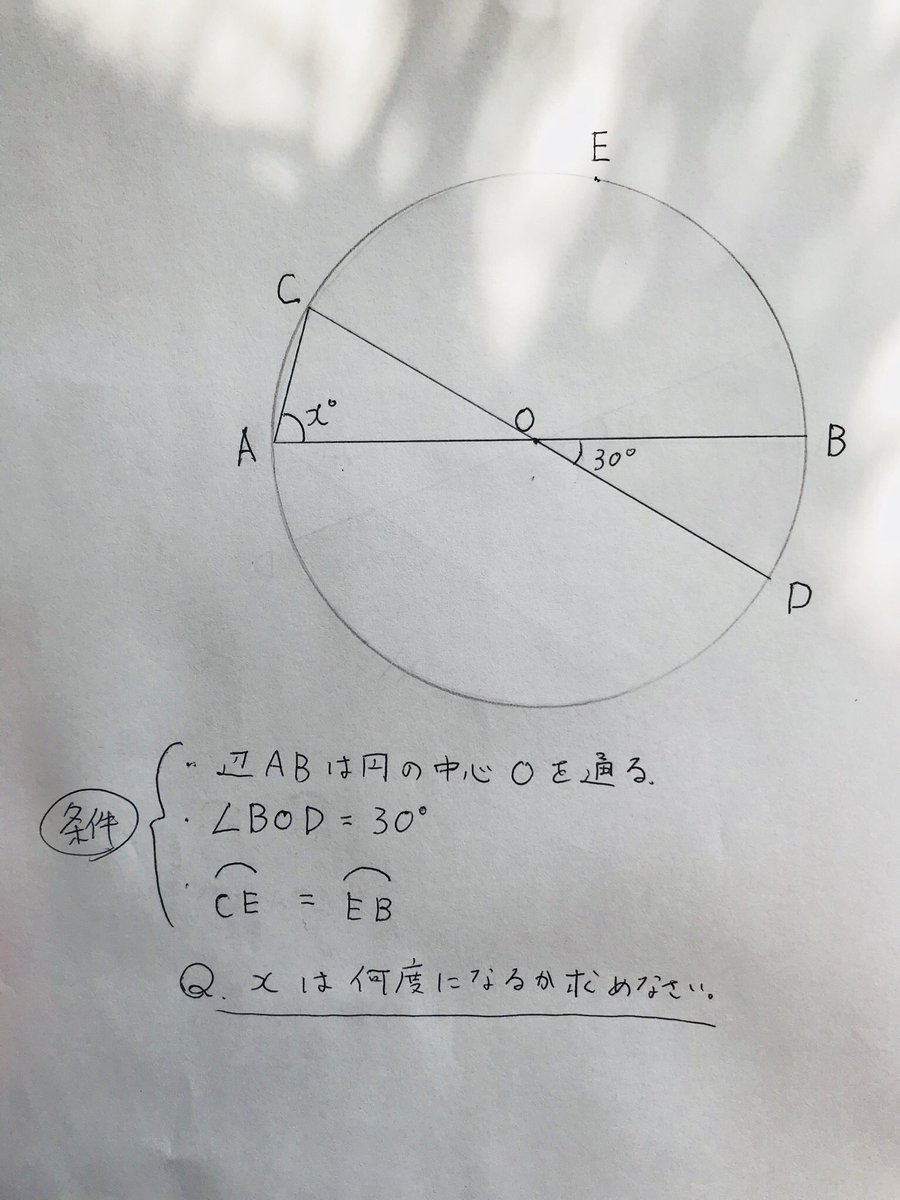



円の性質




数学 中3 56 円周角の定理 基本編 Youtube



1
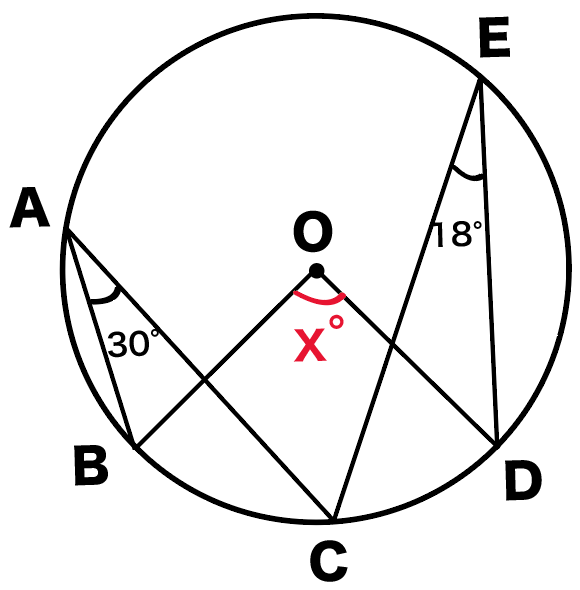



円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく



1
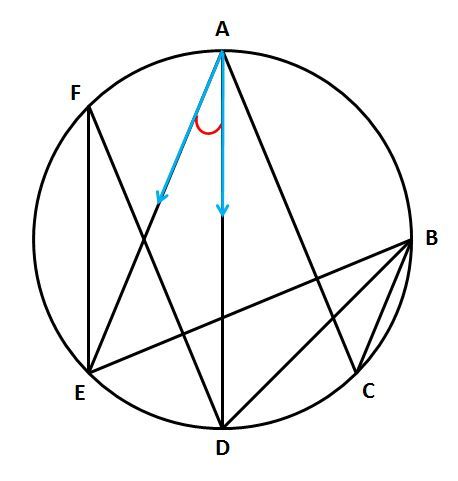



円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室
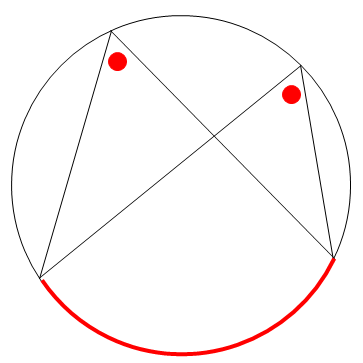



円の性質 3 ネット塾



円周角の定理と中心角 中学3年数学 Youtube




円の性質
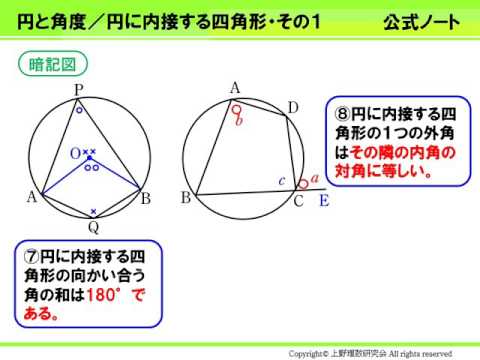



円と角度04 内接四角形の性質 Youtube
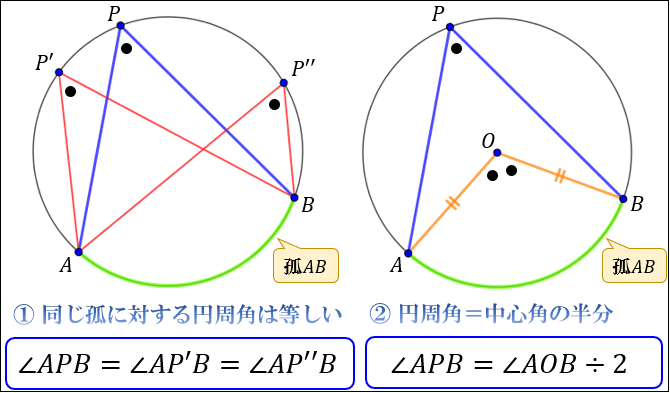



円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ
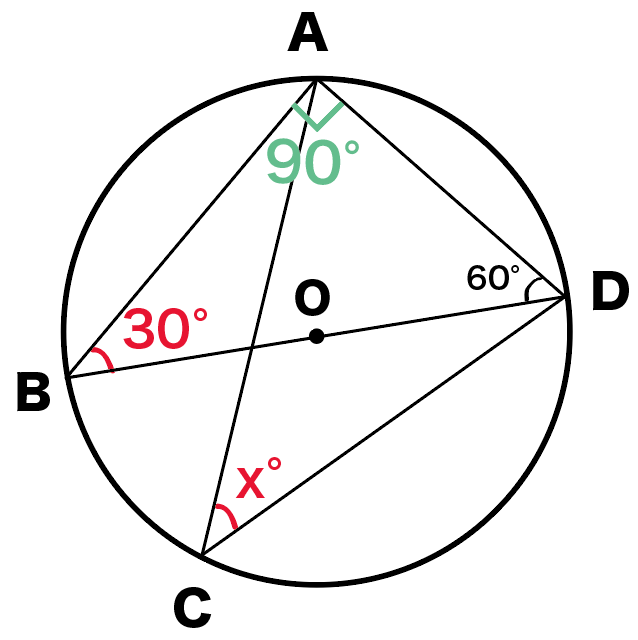



円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく
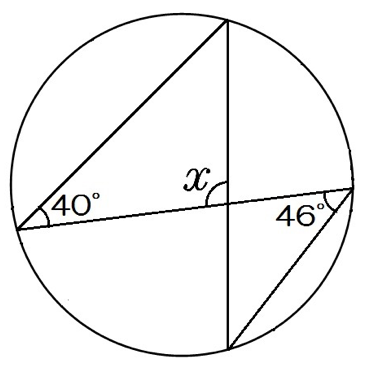



円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ




高校数学a 円周角と中心角のおさらい 例題編 映像授業のtry It トライイット



円と三角形 角度 中学から数学だいすき




数学 中3 57 円周角の定理 少し応用編 Youtube
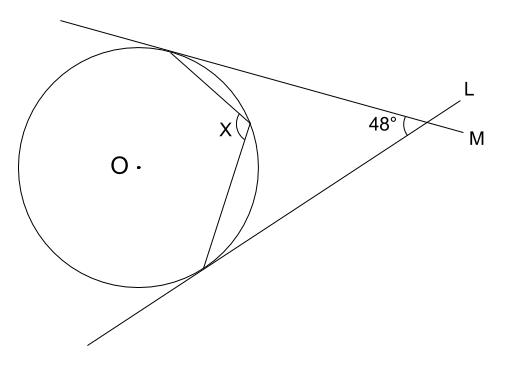



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su
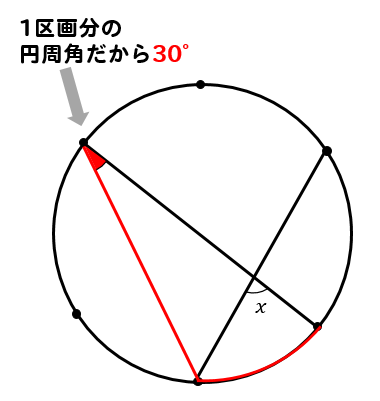



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ
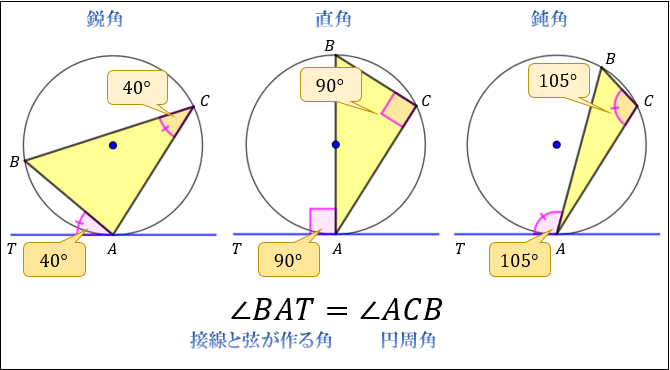



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ
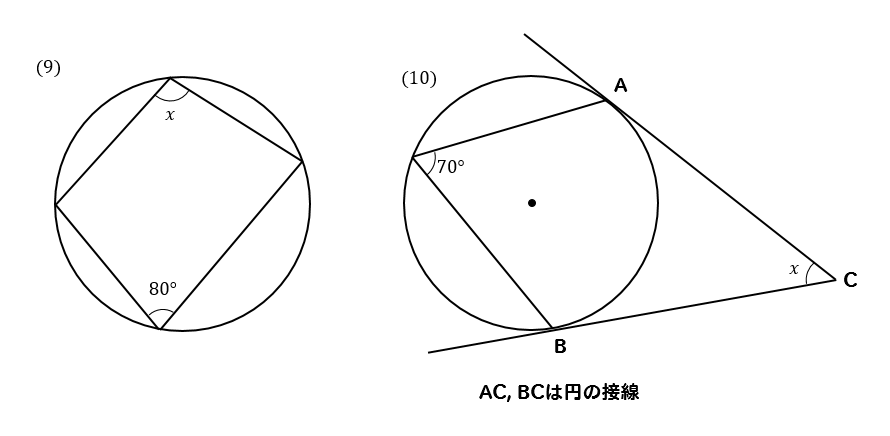



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




円周角の定理 円に内接する四角形等図形の練習問題 中学 高校数学 身勝手な主張



1




勉強しよう数学0 11
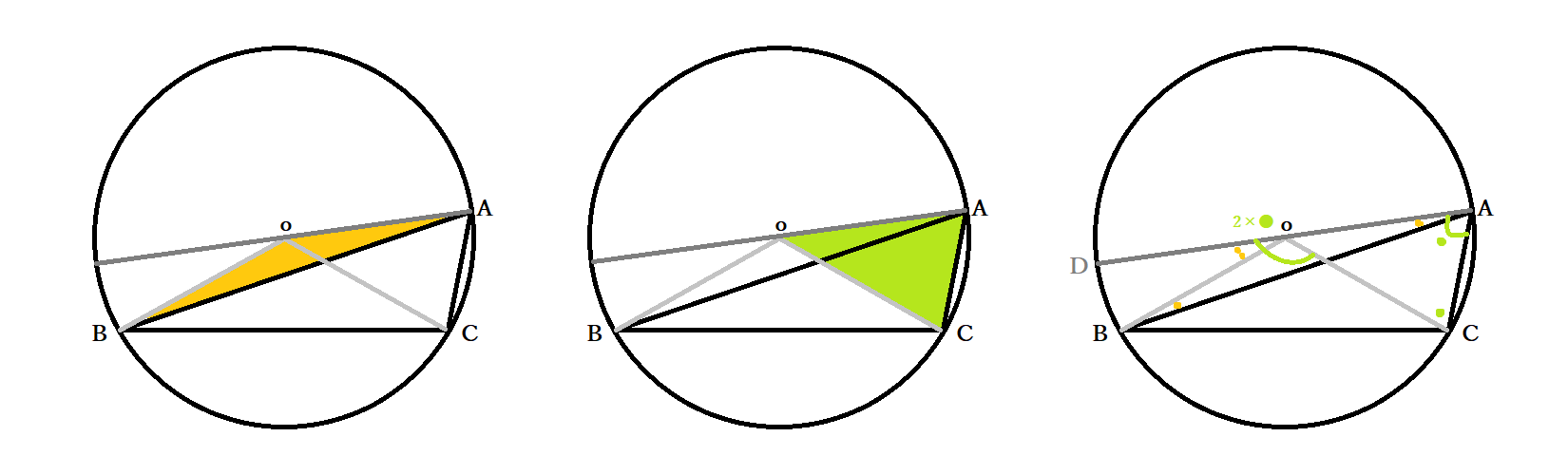



中3数学 円周角の定理とは 円周角と中心角の関係の証明法 円の性質の応用問題 中学 Curlpingの幸せblog



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学




中学数学 円周角 中心角




中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生



中学数学 円周角 中心角



円周角の定理とは 定理の逆や証明 問題の解き方 受験辞典
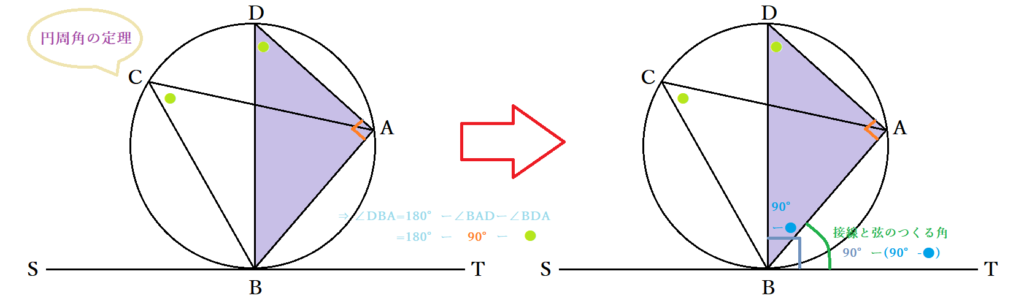



接弦定理とは 接線と弦の作る角の定理の証明 覚え方と応用問題 中学 高校 Curlpingの幸せblog




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者
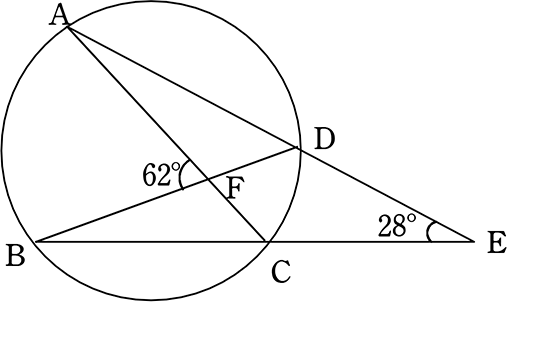



中学数学 円周角 中心角
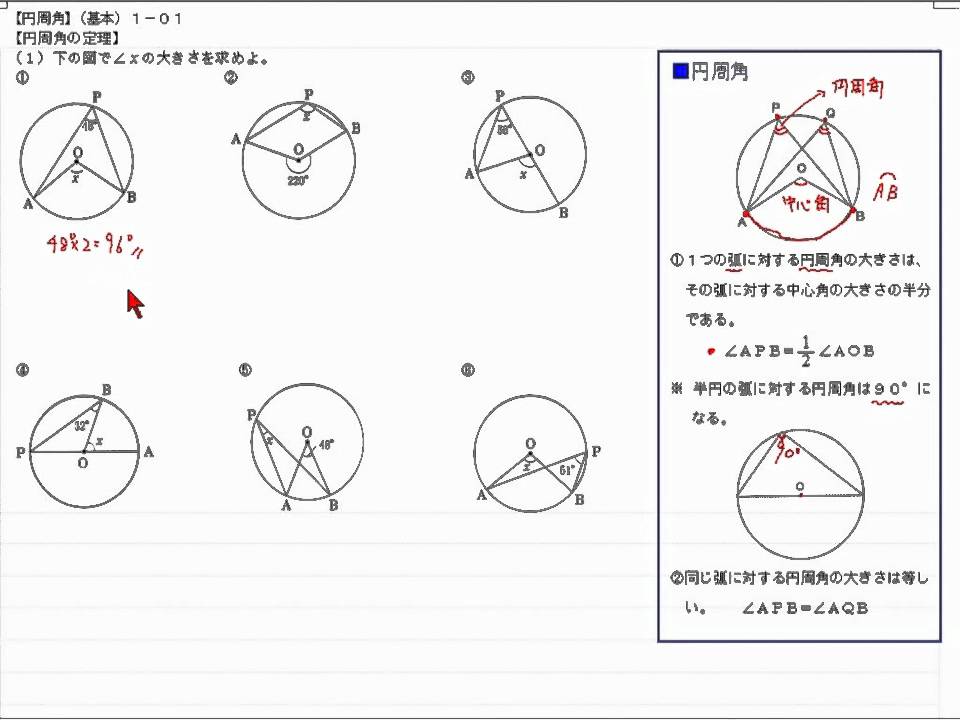



No 295 中3数 円の性質 円周角 基本 1 01 ネット塾の英進塾 Youtube




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




円周角の定理 角度の計算方法と中心角 弧の長さの関係 リョースケ大学




円周角の定理 角度の計算方法と中心角 弧の長さの関係 リョースケ大学




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア
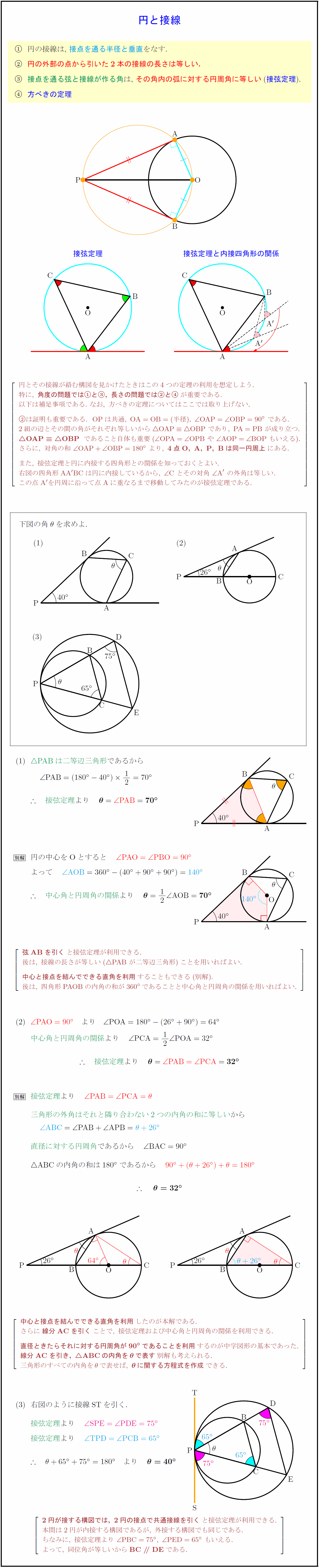



高校数学a 円と接線に関する3定理 垂直 接線の長さ 接弦定理 受験の月
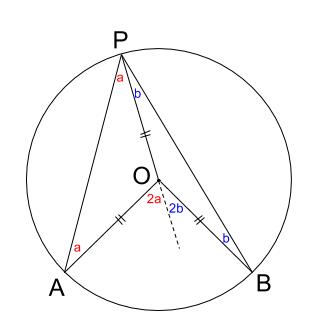



中学数学 円周角の定理はなぜ成り立つのか 中学数学の無料オンライン学習サイトchu Su




接線と円の関係 Jsciencer




円周角の定理とは 必ず押さえたい7つのポイント 遊ぶ数学
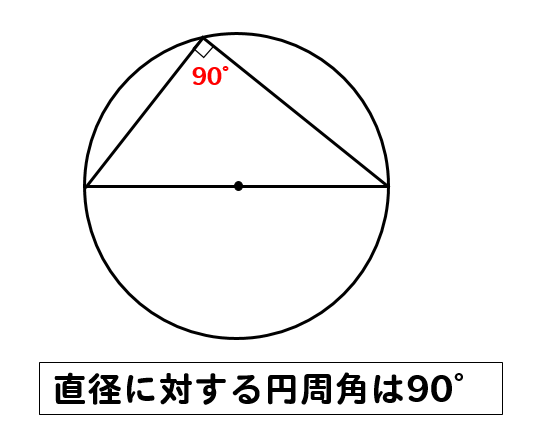



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ




円周角の定理 角度の計算方法と中心角 弧の長さの関係 リョースケ大学
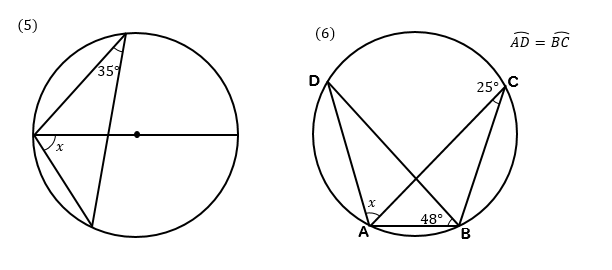



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ
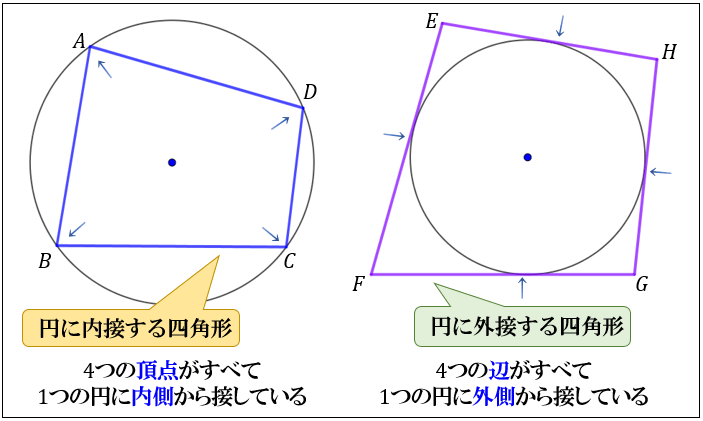



円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ



円の接線と角度 中学から数学だいすき




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者
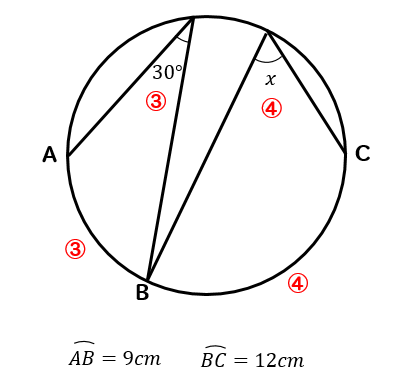



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ
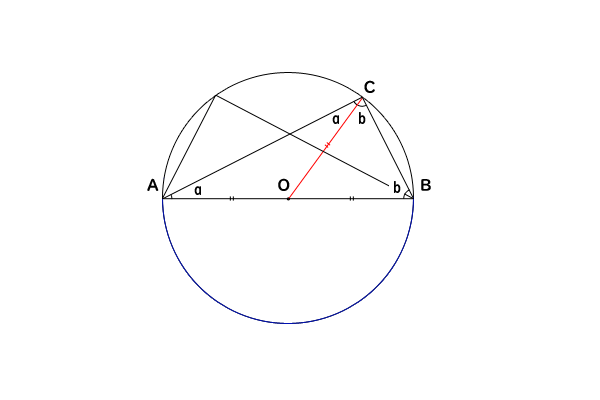



円周角の定理とその逆の証明 高校数学マスター




中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア
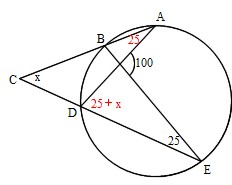



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ




円周角の定理 角度の計算方法と中心角 弧の長さの関係 リョースケ大学



0 件のコメント:
コメントを投稿