関連記事 嫌いな問題,高校数学で楽ちん?② ルーローの三角形(21北海道)(学校裁量問題解説) カモフラ正方形パズル(1998年筑駒) 相似の利用とx^2の消去(19年度大阪府B) 回転(15年裁量問題解説) 第23回 相似は意外とおもしろい! 53K 大人でもちょっと手こずってしまうような、難問奇問が続出する中学入試の算数。 でもだいじょうぶ、コツさえつかめば怖くありません! 学習サポートセンターのカズが、算数を楽しく学ぶ方法を伝授し面白い数学図形問題 (中3) カテゴリ: カテゴリ未分類 中2の K衛門 。 やはりカンどころがよくて、もうすっかり図形の苦手意識がなくなっている。 期末テスト数学は予定通り (? )余裕で100点。 で、先生から数学のライバルの子と2人だけに 特別出された
爲何 嫌疑人x的獻身 數學邏輯卻敗給哲學問題 雪花新闻
相似 問題 難問
相似 問題 難問- 相似問題より→難問ではないのですが・・・(灘中学 12年) 相似の利用→光源と影(聖光学院中学 10年) 相似問題より→面積比と面積(東海中学 惑わす相似(14年度大阪府B) このブログは「高校入試 難問」や「高校入試 数学 良問」などで検索して来られる方が多いです。 ということで,久々に芸術的な,中学数学の問題をご紹介します。 今回は, 14年度大阪府Bの問題 です。 えげつない問題




19 H31 年度公立高校入試 正答率が低い難問 数学の解説と練習問題
そこへの対策問題としても活用できる問題を選びました。 問題+解説難関私立対策⑤相似(平面図形)公立図形満点目標の準備問題pd PDFファイル 19 MB ダウンロード難問に挑戦(第11回算数オリンピック、ファイナル問題) (4)までは解かない方がいい問題(清風南海中学 08年) 補助線はどこに? (大妻中学 10年) 平行線を利用した相似問題(栄東中学東大クラス選抜 10年) かげの長さ(日本大学第一中学 10第3学年 5 図形と相似 知識・技能の習得を図る問題解答 年 組 号氏名 練習問題⑤ 相似な図形の面積の比 相似な図形で,相似比が m:n ならば,面積の比は m 2:n である。 1 25:49 ポイント 相似比が5:7だから,面積の比は52:72
相似条件はしっかりと覚えておきましょう。 それでは これからの相似条件を使って 相似な図形を見つける練習をしましょう。 相似な図形を見つける問題 それでは、良く出てくる問題に挑戦してみま 21世紀最難問 21世紀は平均点05を下回る問題がバンバン出ています。→数学オリンピックの合格点推移 平均点と完答者数を考慮して自分が過去最難問だと思ったものを紹介します。09年 imoドイツ大会 第6問です。 中3 数学 超難問 中学生 数学のノート Clear 表紙 1 2 3 公開日時 16年12月01日 22時02分 更新日時 年06月25日 時38分 中学生 3年生
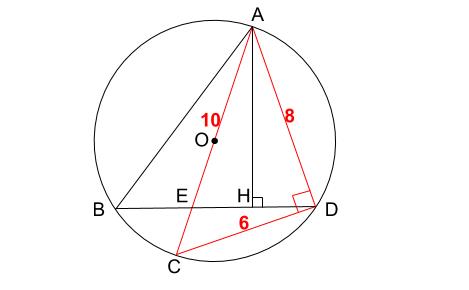
ついに出ました! 正解率0%です。 平成25年度 岐阜県 数学 問4 (2)(イ) 正解率 0% 上の図で、4点 a、b、c、d は 円o の周上にあり、ac は 円o の直径で、ah は 三角形 abd 中学の数学の難問の解き方 基本問題やそこまで難しくない応用問題(典型問題)を完璧にする 問題に応じてどの解法を使うかを整理しておく 難問に対して解法を順に使っていく 数学の難問を解くときの2つのコツ 与えられた条件をすべて使う 解く道筋 相似な図形の体積比の問題です。 基本を確認して、いろいろな応用問題を解けるようにしてください。 基本事項 相似比が a b である図形の面積の比は, a3 b3 である。 *簡単な証明もできるようにしましょう。
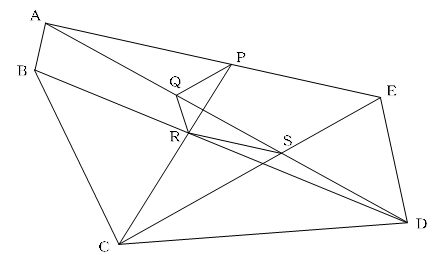



第4回 図形問題に強くなる 相似の発見 算数ドクター




辺の比 面積比 相似 16年東京都 高校入試 数学 良問 難問
相似分野の応用問題①ラスボスっぽいの,多分それ連比です。 面積の比 (何倍)を求める問題も含めてかんたんな方法を解説します 教遊者 IC Channel 192K subscribers Subscribe 中3相似「相似分野の応用問題①連比面積の比 (何倍)‐かんたんな方法を解説 この問題は①②とも点光源による影について問う典型的なものですが、発した光が不透明な面の各頂点をかすめて平面 α 上のどこに影を投ずるのか、相似を利用して線分比をしっかり計算していきましょう。 解答・解説 問題文に書いてあって、まだ使っていないこと、(1)(2)を解いている途中で分かったこと、これらの中から、パズルを解くための鍵を探すしかありません。 答えは、 ずばり、 三角形 \(ade\) と三角形 \(ceg\) の相似です。 一番はじめに注目した相似です。




第14回 東大生も悩む 図形問題 Z Square Z会
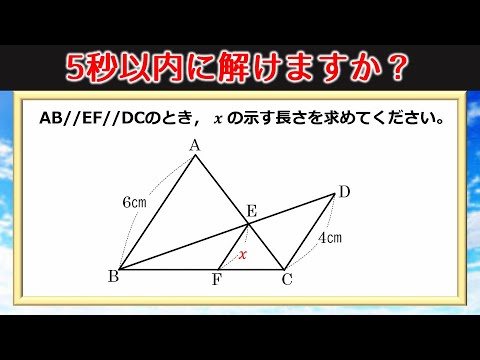



図形問題 知っている人は5秒で解ける相似の裏技 Youtube
相似な図形のかき方、三角形の相似条件や、相似を利用した距離や高さの求め方を練習していきます。 プリント6枚 中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード・印刷 史上最難問10題 ギズモード・ジャパン 解けるかな? 史上最難問10題 00 24,0 satomi これ開いたってことは自分は賢いと思って数学35章図形と相似「相似な図形」<基本問題①> 組 番 名前 A B C E (1)辺BCに対応する辺を答えなさい。 (2)四角形ABCDと四角形EFGHの相似比を求めなさい。 (3)辺EFの長さを求めなさい。 A D B C 60° 6cm 8㎝ E H F G 80° 6cm



17年12月 哆嗒数学网 博客




中学校 数学 3年 5章 5 三角形の相似の証明 定番問題演習 実践編 ワカデキな中学校数学
こんにちは!レオンです。 今回はある裏技をご紹介したいと思います(*´ω`*) 後ほど簡単な例題も紹介するので、そちらもぜひ見ていって下さい~ 裏技の説明 証明 ① adcと cbeの相似 ② 面積比 a b ③ aedと abeと ebc ④ dec 例題 問題 答え まとめ 裏技の説明 それでは詳しく見て図形問題 122 152K 大人でもちょっと手こずってしまうような、難問奇問が続出する中学入試の算数。 でもだいじょうぶ、コツさえつかめば怖くありません! 学習サポートセンターのカズが、算数を楽しく学ぶ方法を伝授します 由井中の中間テストの数学に超難問が・・・ こんにちは、みなみ野教室の横山です。 今日10/2で由井中の中間試験が終わりますが、数学が終わり、中3の生徒が・・ 先生この問題見て、と・・・・ 1問だけですが、ヤバイやつ (問題)が・・・ 問 を解け



Math 空間図形と相似 面積比 体積比 発展問題 働きアリ The 2nd
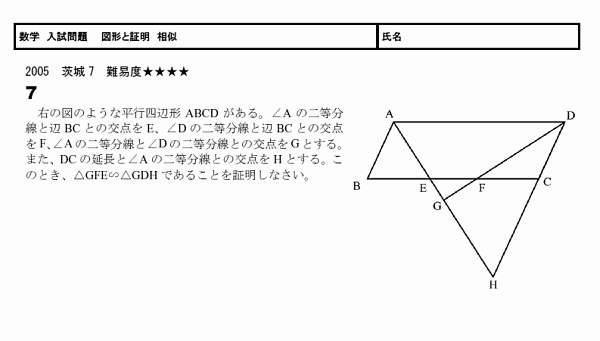



図形と証明 相似 無料学習プリント教材
芸術的な難問 良問数学 中2数学 複雑な多角形 角の和応用問題 今回は複雑な多角形の角の和の問題とその考え方です 星型など複雑な図形の角の和を求めるとき三角形の外角の定理やブーメラン型四角形の角リボン型ちょうちょ型の三角形の角の考え方が役立ちます こんにちは!レオンです。 今回はこの問題を解いていこうと思います(*´ω`*) 見た目はシンプルで一見簡単そうに見えますが、かなりの難易度だと思います。 さすが灘 (*´Д`) ヒント 答え 詳しい解説 ①補助線を引く ②abの長さを求める ②1 相似を見つける ②2 de ea = bd ba ③三平方の 応用問題を解くには、当然、基本が分かっていないとできません。 ということで、まずは相似(合同)や比の問題で最初にやることを確認しておきます。 ①与えられた長さ、角度、比は図に書き込む ②比を求めたい場合は、比を求めたい直線を、1辺とし



相似 これが中学入試に出た図形問題




中3 数学 超難問 中学生 数学のノート Clear
今回の問題の結論は、 ABE∽ CBD となること これが言えるために必要な条件は、 3組の辺の比が全て等しい 2組の辺の比とその間の角が等しい 2組の角が等しい だね。 ここは覚えていないといけないところ ここが分からない人は、 証明じゃなくて 相似 平行線が作る2つの三角形は相似になります。 ※相似の問題の解法の応用問題をご参照ください 相似から線分比を使って求めます。 (1)の図形は度々定期試験等で出題されます。『相似な図形』の単元の中から 平行線と線分の比という内容について解説してきます。 ここでは、相似な図形の性質をつかって いろんな図形の辺の長さを求めていきます。 長々と解説をするよりも 問題を見ながら、実践を通して学習するのが良いので



さすらいのおやじ数学難問集




最も選択された 相似 問題 難問 ニスヌーピー 壁紙
相似で相似比 は2:1。 2:1=12cm:ac。 ac=24cm。 三角形aegと 三角形cdgは 相似で相似比 は1:2。 三角形ahdと三角形chfは相似で相似比は2:1。 の比と の比を でそろえると、ag:gh:hc=1:1:1。 gh=24÷3=8cm。補充問題に塾技66 難問「円と相似」を追加しました。 補充問題に塾技21「座標平面上の四角形(1)」を追加しました。 補充問題に塾技34 難問「展開の応用」を追加 問題 ★ 次の図で、ab=40,ac=30,bd=である。 (1) aebeを求めよ。 (2) aeを求めよ。 ヒント、着眼点 高校入試で2つの線分の長さの比を問われた時は、2つの三角形の面積比から持ってくるか、相似な2つの三角形の相似比から持ってくることが多いです。



Homeroom 数学の入試問題を解くとき大切なこと 正しい入り口から入らないと問題は解けない 平面図形 相似 働きアリ



空間図形問題 難問 個別指導塾arrows講師ブログ
合同と相似の証明問題の流れ 合同や相似を証明する問題の解き方についてです。 解答すべき内容が示されているので比較的得点しやすい問題になります。 練習を重ねて解けるようになりましょう! 記事を読む




勉強しよう数学 10月 17



U9j580gf8iba369ji2w Xyz P 1516




相似 平行四辺形と面積比の問題を徹底解説 数スタ




中3数学 三平方の定理 図形問題 愛知県公立高校入試 難問 Youtube




面白い数学の問題 ラングレーの問題 難問注意 だが面白い そらの暇つぶしch



觀無量壽佛經疏妙宗鈔 宋四明沙門知禮述
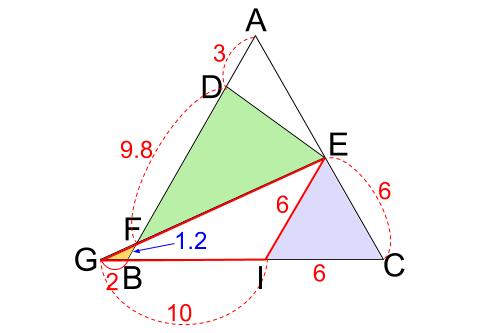



難問 正三角形の相似 中学数学の無料オンライン学習サイトchu Su



U9j580gf8iba369ji2w Xyz P 1392



大人は解けない 超難問 第9回算数オリンピック ファイナル問題より どう解く 中学受験算数



高校入試数学の難問 円 相似と三平方の定理の総合 中学数学の無料オンライン学習サイトchu Su




中学生でも解ける外伝 高校入試難問35 灘高 日比谷高校のススメ



超難問 ジュニア算数オリンピック ファイナル 09年 どう解く 中学受験算数




高校入試対策問題集 合格への最短完成 数学 Amazon Com Books



Test Article Tech News




中学数学平面図形 公立高校入試の良難問 定期テストや高校入試に レオンの中学数学探検所




中学数学 相似な図形の証明問題のコツ ちょい難問 なぜか分かる はかせちゃんの怪しい研究室




中学数学平面図形 公立高校入試の良難問 定期テストや高校入試に レオンの中学数学探検所




灘中2020年 相似ー 中学受験算数の良問 難問 基本問題
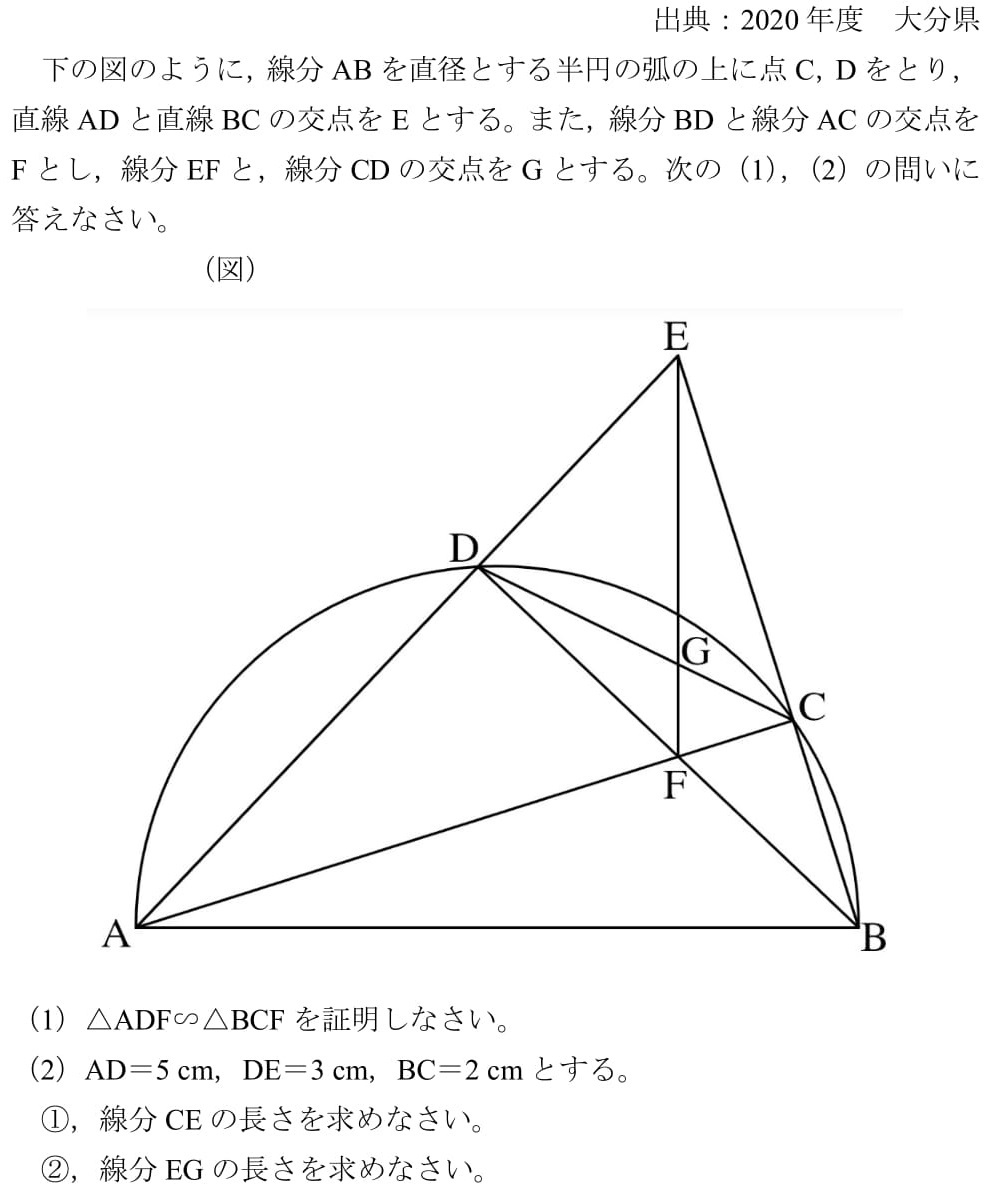



正答率0 4 見えざる相似 大分県 高校入試 数学 良問 難問




超難問ぞろい Exile エグザイル ファンクイズ 相似应用下载 豌豆荚
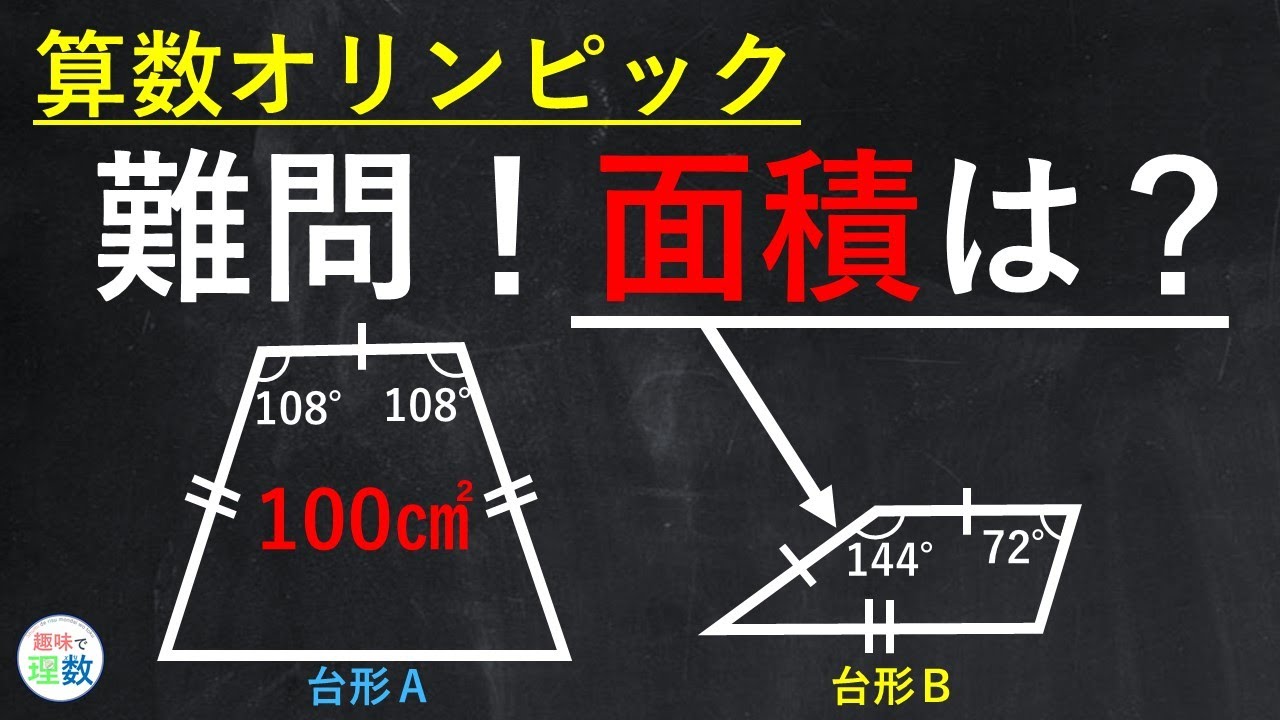



超難問 この問題を解ける人凄い 算数オリンピック 勉強 Youtube スタディチューブ




建構你的自動化學習知識體系 讓你提升一倍閱讀量 在這樣資訊爆炸的時代 人們在職場中的壓力也隨之上漲 因為我們進入了前所未有的需要 By 為你而讀



爲何 嫌疑人x的獻身 數學邏輯卻敗給哲學問題 雪花新闻
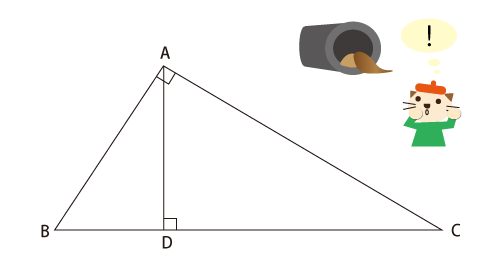



第14回 東大生も悩む 図形問題 Z Square Z会
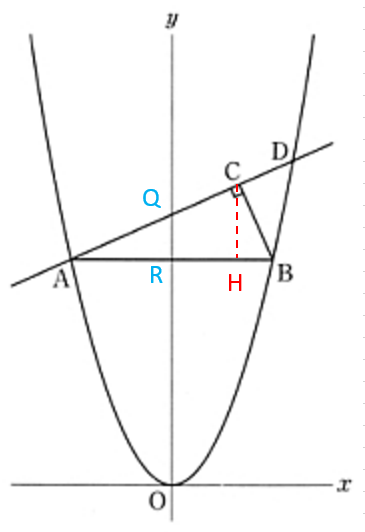



高校入試超難問 平成24年 埼玉県数学 問3 正答率 0 4 の解説 偏差値40プログラマー




相似な図形の応用問題を洛南高校の数学難問で 超難問の高校入試 Youtube




中3数学基礎 本当に使える裏技 相似の問題で差をつけろ 定期テストや高校入試に レオンの中学数学探検所




年度中学入試 平面図形の最難問 東大カリスマ塾長 浜田一志公式ブログ 9割が伸びる 文武両道 勉強法
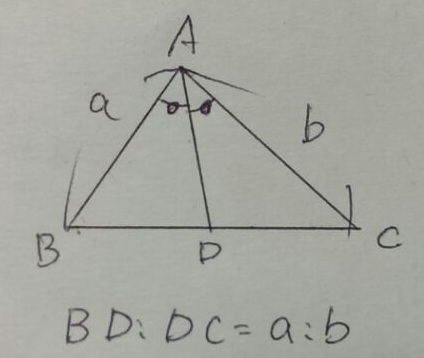



16年度 茨城県公立高校入試 数学 解説 家庭教師サボの部屋
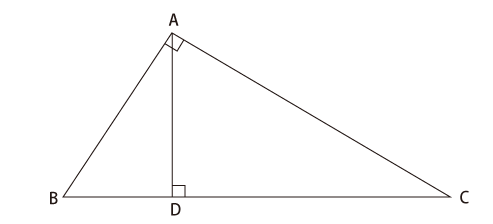



第14回 東大生も悩む 図形問題 Z Square Z会
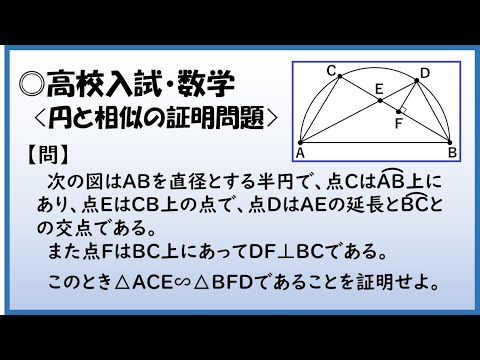



高校入試 数学 円と相似の証明問題 Youtube
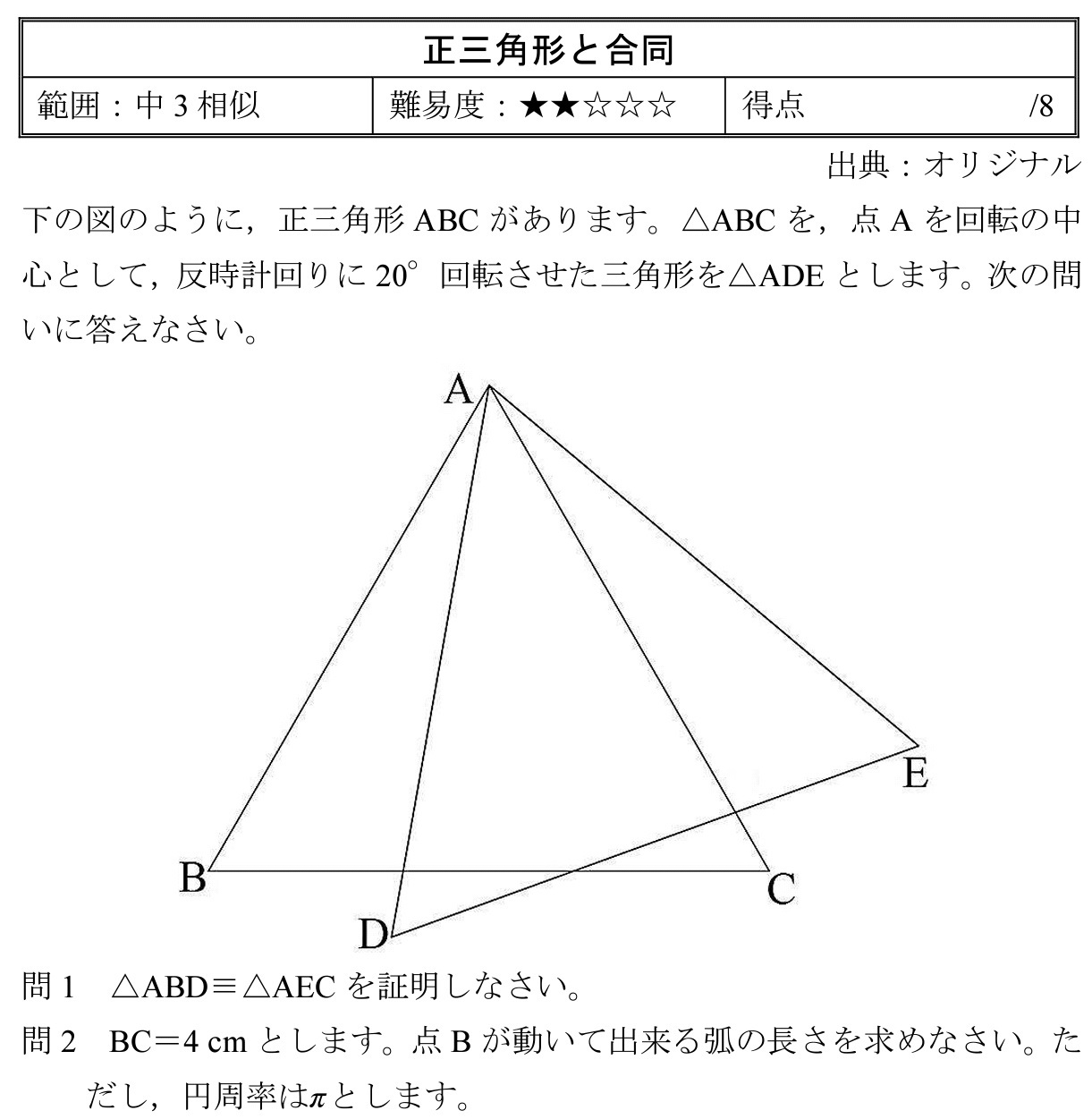



訂正 正三角形と合同 高校入試 数学 良問 難問
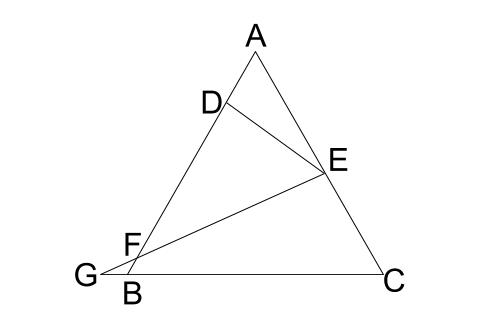



難問 正三角形の相似 中学数学の無料オンライン学習サイトchu Su




太極拳理論家陳鑫之學拳須知的要義 探悟 質疑 資訊咖



平面図形の難問1 日大豊山中




19 H31 年度公立高校入試 正答率が低い難問 数学の解説と練習問題
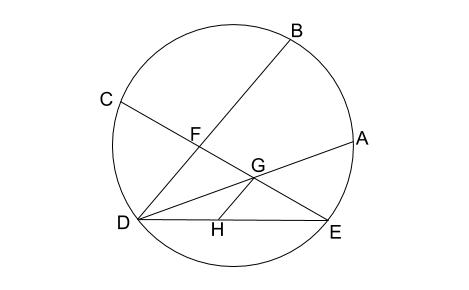



円の総合問題 その5 相似の利用の難問 中学数学の無料オンライン学習サイトchu Su




Math 相似 相似の難問を ちょうちょ と おむすび で簡単に解く 2 働きアリ



中学数学の難問です 解き方がわからない為 数学が得意な方教えて頂け Yahoo 知恵袋



中学数学で 円と相似の難問が載っているサイトがあれば教えて下さい Yahoo 知恵袋




客看屋被要求裝朋友 眾揪暗黑疑點



平行線を利用した相似問題 栄東中学東大クラス選抜 2010年 どう解く 中学受験算数
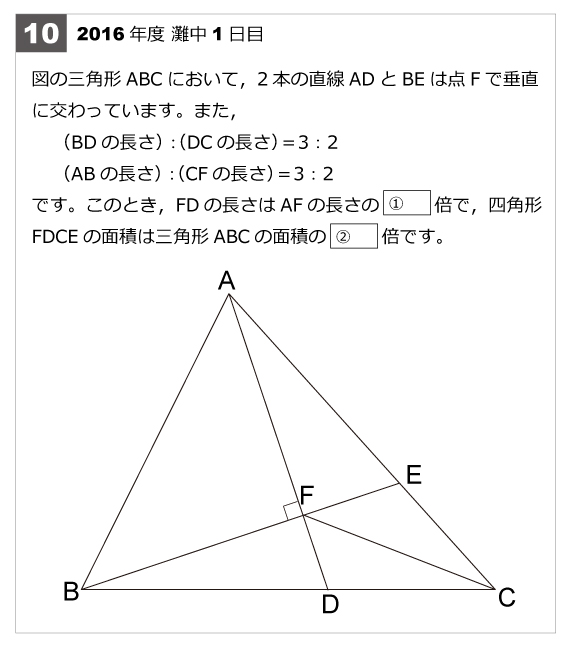



灘中解説速報 16年第10問 平面図形 難問 算数星人のweb問題集 中学受験算数の問題に挑戦



中3 数学相似比 ニスヌーピー壁紙




Myjapan 最專業的日本雅虎yahoo 代標 日本樂天rakuten代購 日本雅虎yahoo 代購服務 擁有日本代標代購10年經驗




19 H31 年度公立高校入試 正答率が低い難問 数学の解説と練習問題
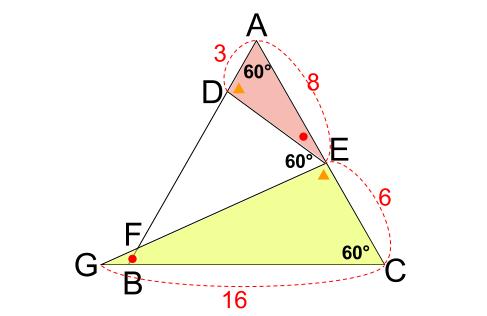



難問 正三角形の相似 中学数学の無料オンライン学習サイトchu Su



入試問題に挑戦 平成25年度岐阜県 数学 超難問 正答率0 時習館 ゼミナール 高等部




Ftir 原理簡単pm rbmi




中学数学 相似な図形の証明問題のコツ ちょい難問 なぜか分かる はかせちゃんの怪しい研究室



高校入試数学の相似な図形の応用問題を超難問で 洛南高校の過去問を解説 猫に数学




中学数学 相似な図形の証明問題のコツ ちょい難問 なぜか分かる はかせちゃんの怪しい研究室
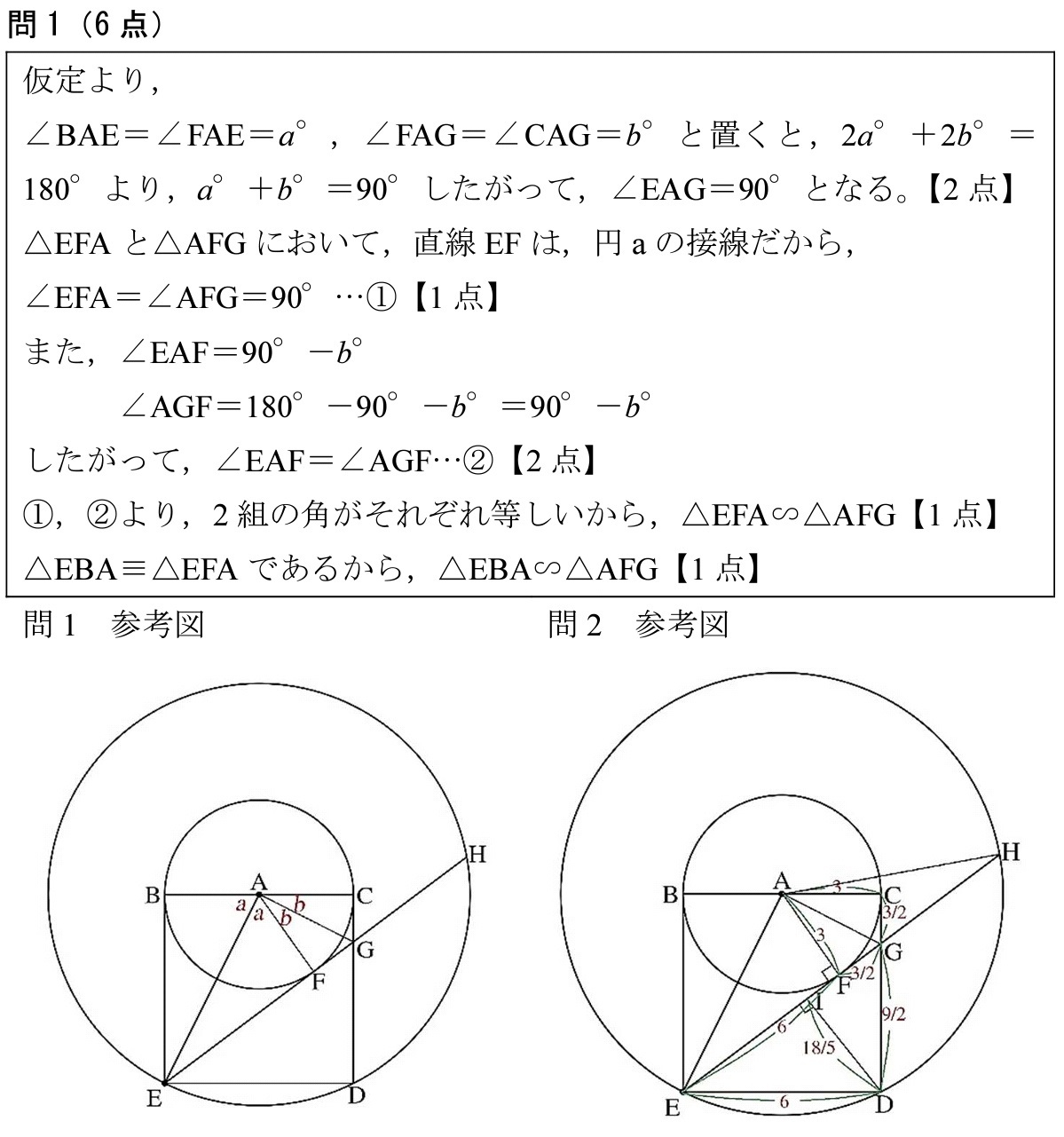



ひたすら難しい相似証明 オリジナル 高校入試 数学 良問 難問
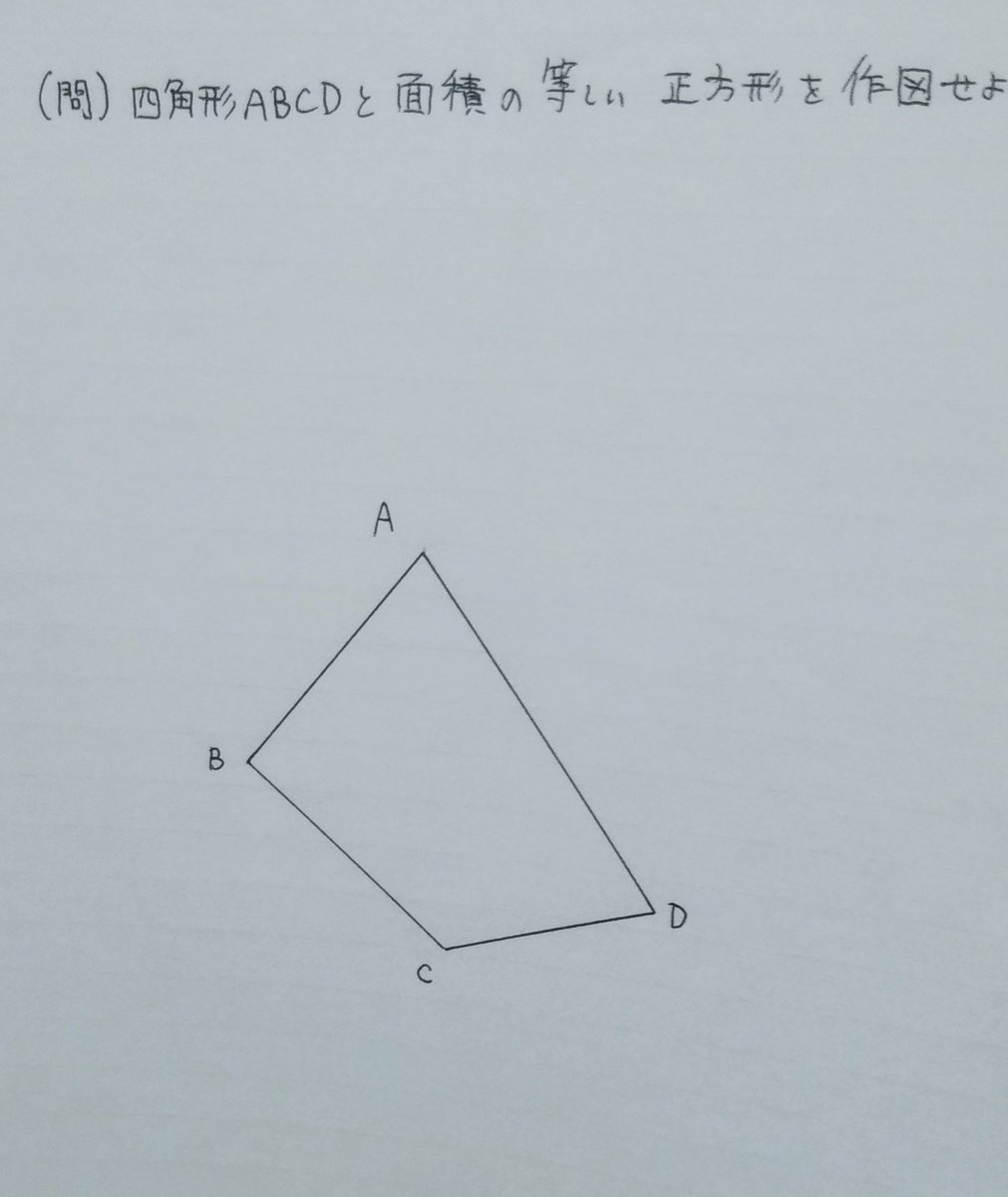



ベリースライム A Twitter 中学数学における作図の最高峰 中3までの知識で作図できます 平方根 2次方程式 相似 円周角 三平方の定理を含むスーパー問題 知っている方も暇つぶしにどうぞ 数学 作図 難問
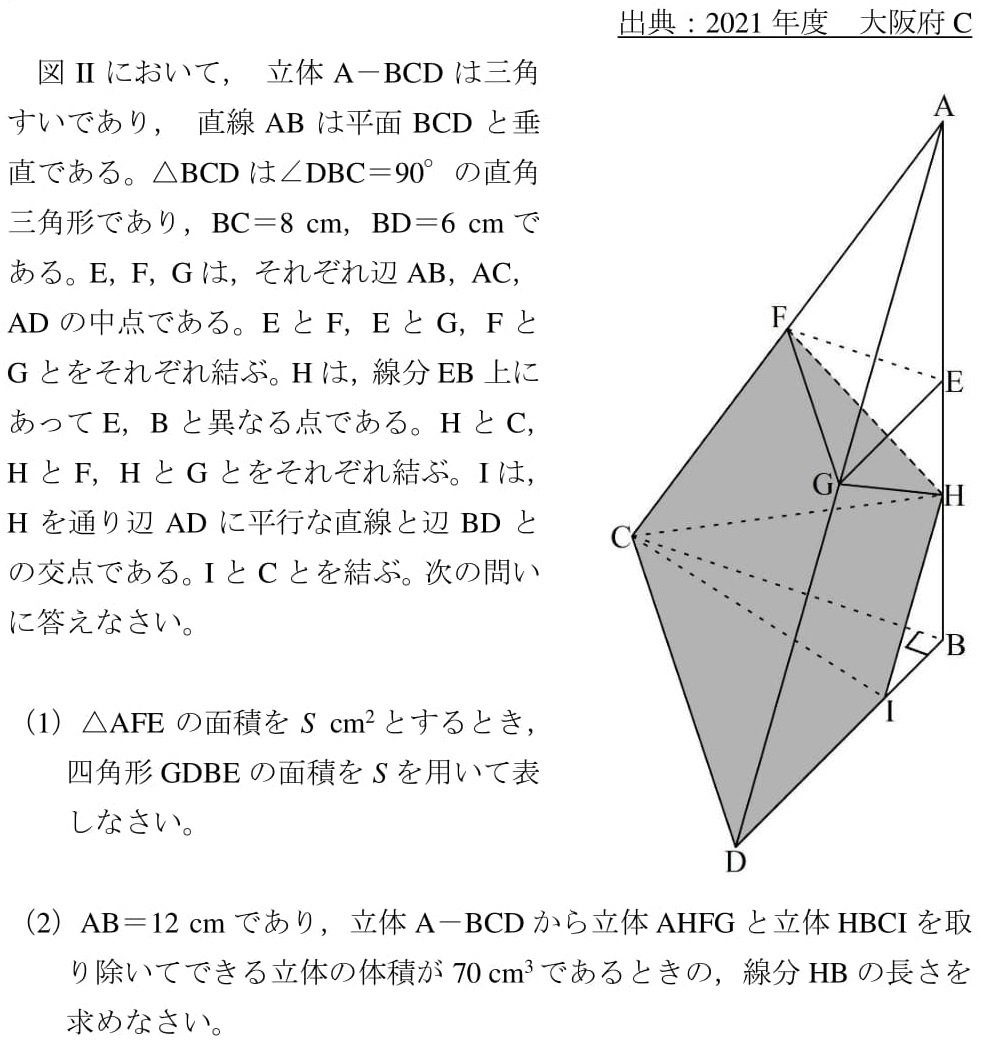



21年大阪府c 相似と面積比 体積比の練習 高校入試 数学 良問 難問




洛南高附中2019年 相似 面積比ー 中学受験算数の良問 難問 基本問題
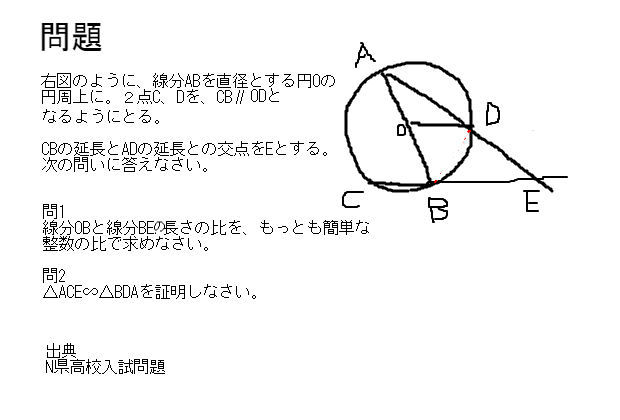



図形の相似問題 中学数学 理科 寺子屋塾の復習サイト




武漢肺炎全球抗戰生技業者 疫苗今夏前難問世 國際 自由時報電子報




年度中学入試 平面図形の最難問 東大カリスマ塾長 浜田一志公式ブログ 9割が伸びる 文武両道 勉強法




Math 相似 相似の難問を ちょうちょ と おむすび で簡単に解く 2 働きアリ
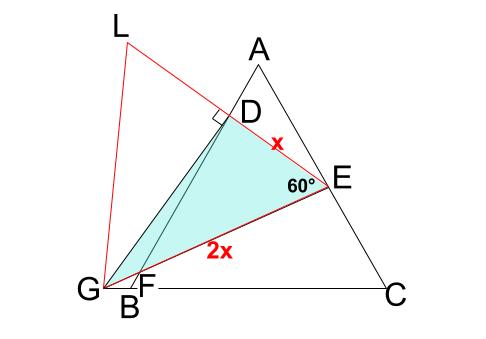



難問 正三角形の相似 中学数学の無料オンライン学習サイトchu Su




意外と解けない相似問題 中3教科書レベルの基本問題 暇つぶしに動画で脳トレ



Math 相似 相似の難問を ちょうちょ と おむすび で簡単に解く 1 働きアリ




勉強しよう数学 高校入試の難問の解き方
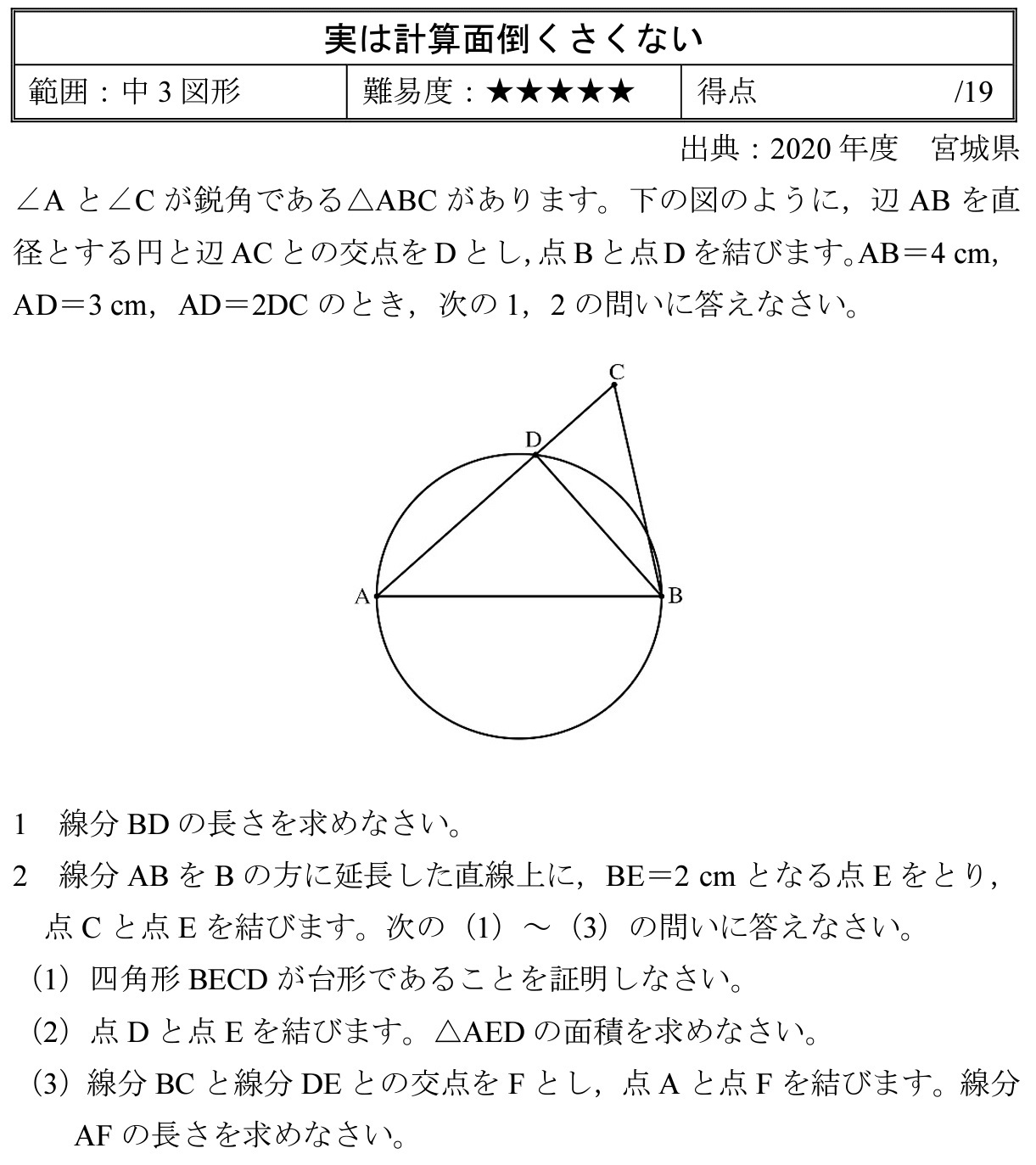



面積比難問 チェバの定理は禁止 年度宮城県 高校入試 数学 良問 難問




角度 図形問題 相似を作る 数学難問 中学入試 Youtube




楽天ブックス 高校への数学 19年 10月号 雑誌 学参 東京出版 雑誌



相似問題より 難問ではないのですが 灘中学 2012年 これが中学入試に出た図形問題



相似 これが中学入試に出た図形問題




相似な図形 補助線を引いて考える相似の問題 中学生からの勉強質問 数学 進研ゼミ中学講座
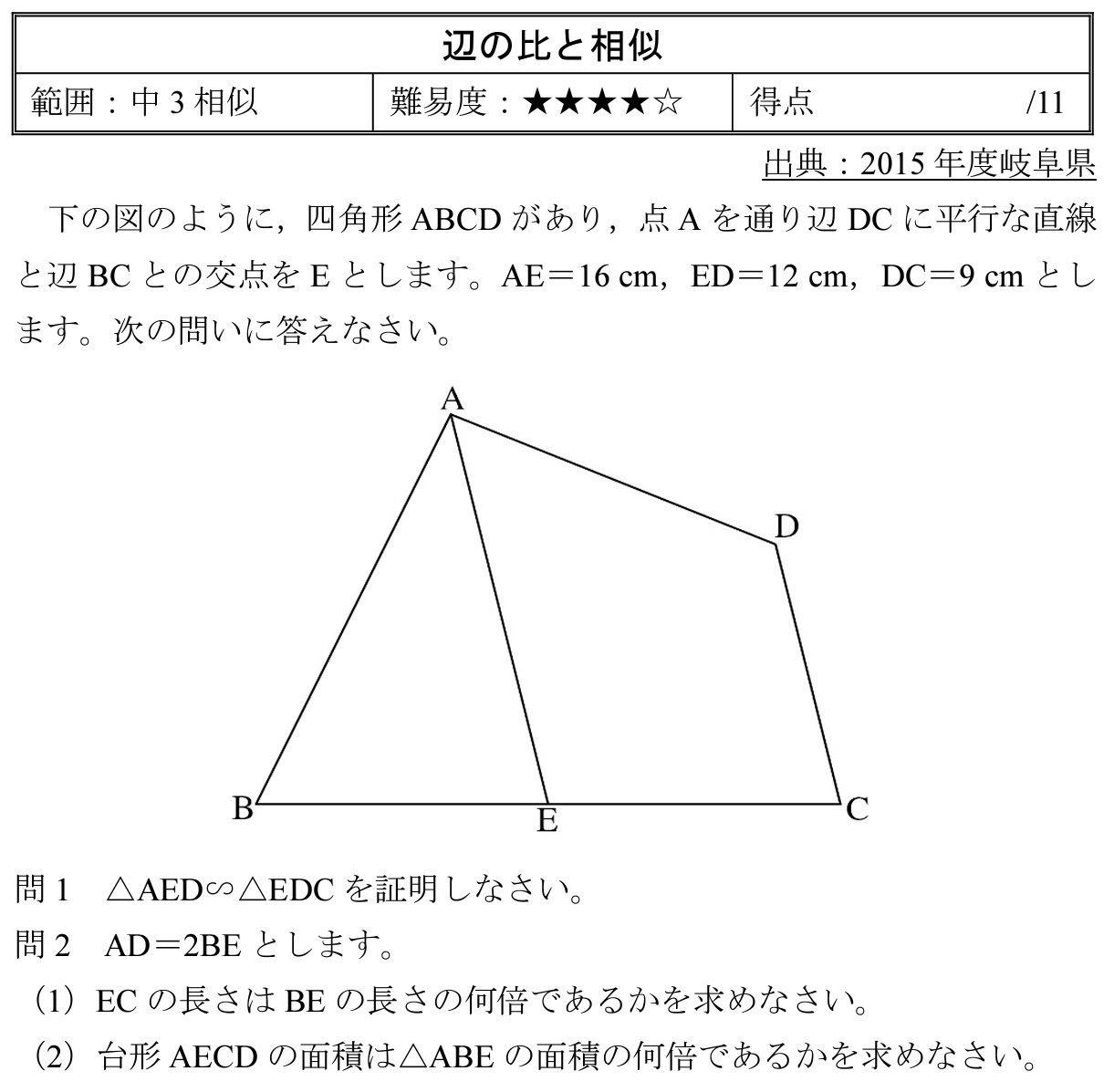



相似比辺の比 15年度岐阜県 高校入試 数学 良問 難問



中学数学のの相似と円の難問 山形の中3です 羽黒高校専願なんですが こ Yahoo 知恵袋
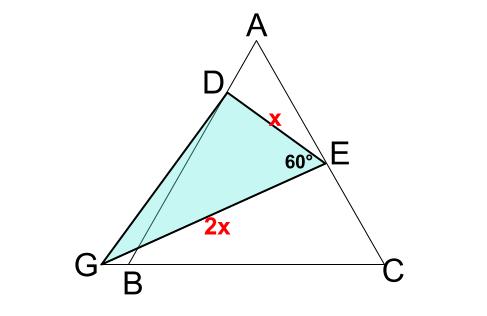



難問 正三角形の相似 中学数学の無料オンライン学習サイトchu Su




中学数学 正答率2 1 公立高校入試で出た平面図形の難問 定期テストや高校入試に レオンの中学数学探検所



相似を使う問題 難問に挑戦 第11回算数オリンピック ファイナル問題 中学入試算数68分野別解法




四天王寺中2020年 相似ー 中学受験算数の良問 難問 基本問題



高校入試数学の相似な図形の応用問題を超難問で 洛南高校の過去問を解説 猫に数学
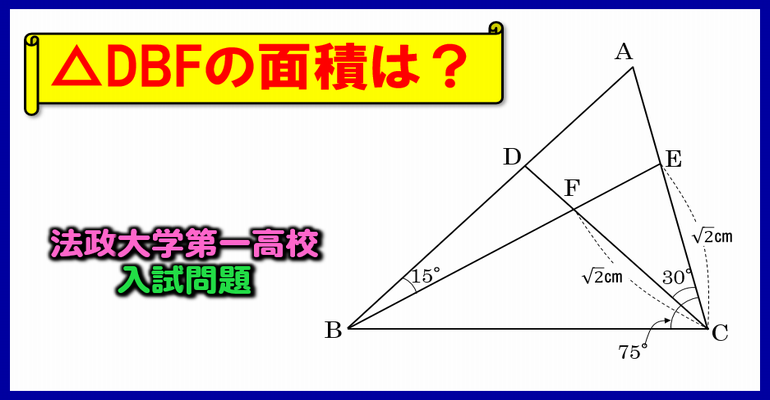



高校入試問題 全2問 難問ですが良問 子供から大人まで動画で脳トレ 楽天ブログ




勉強しよう数学解答集 相似図形の難問の解き方
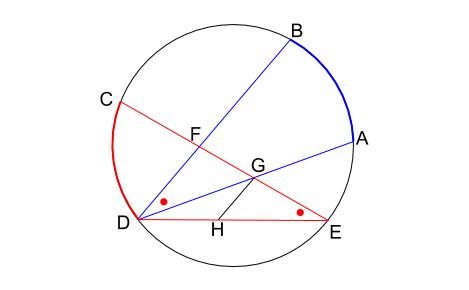



円の総合問題 その5 相似の利用の難問 中学数学の無料オンライン学習サイトchu Su
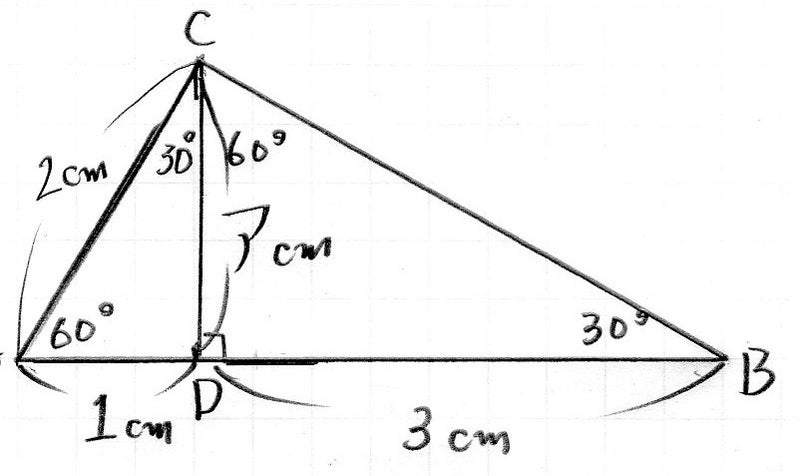



年度中学入試 平面図形の最難問 東大カリスマ塾長 浜田一志公式ブログ 9割が伸びる 文武両道 勉強法
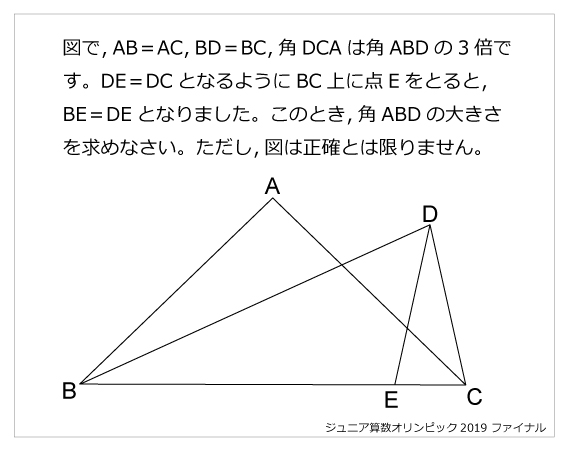



二等辺三角形 算数星人のweb問題集 中学受験算数の問題に挑戦




Koko Heno Sugaku October 12 Amazon Com Books
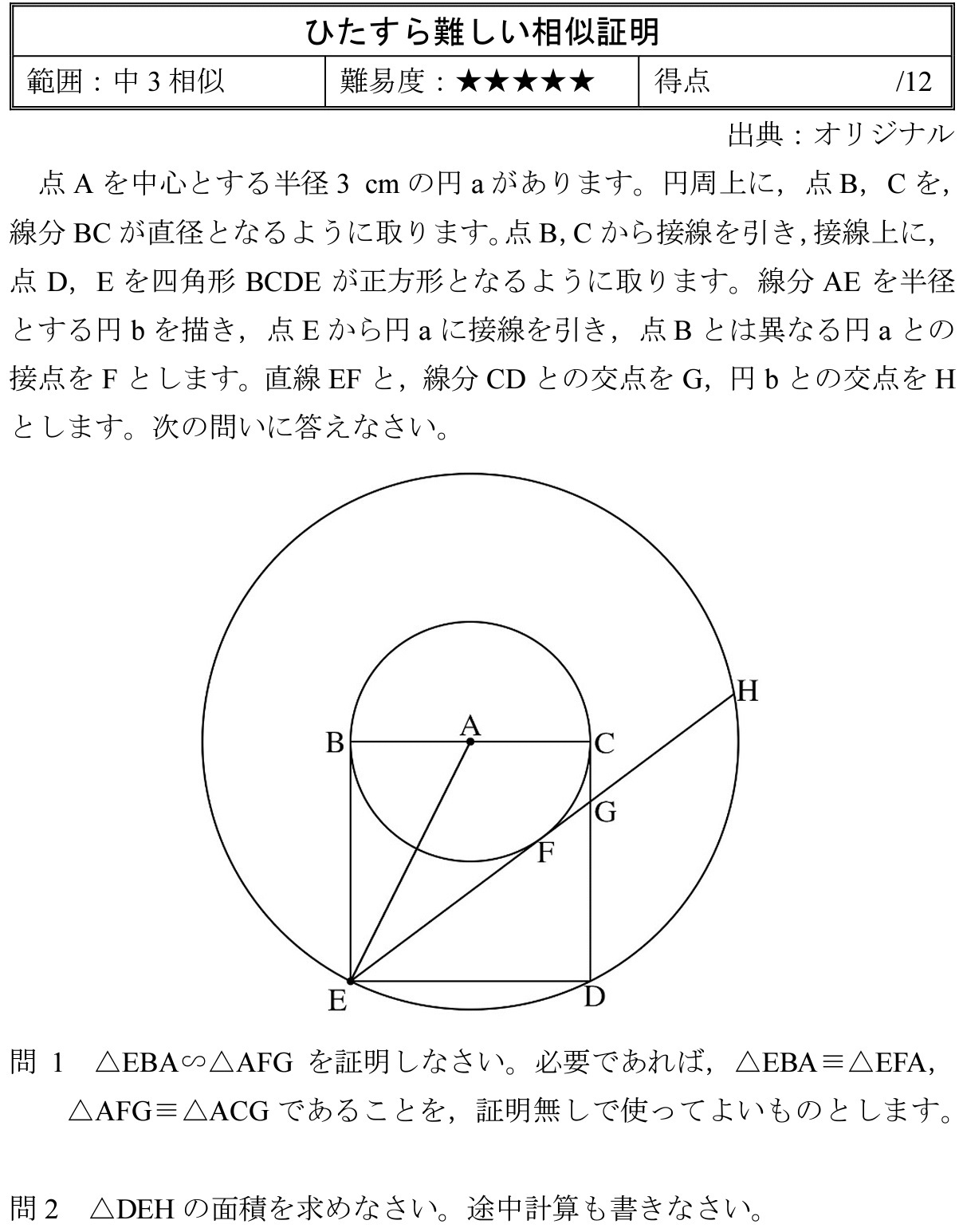



ひたすら難しい相似証明 オリジナル 高校入試 数学 良問 難問
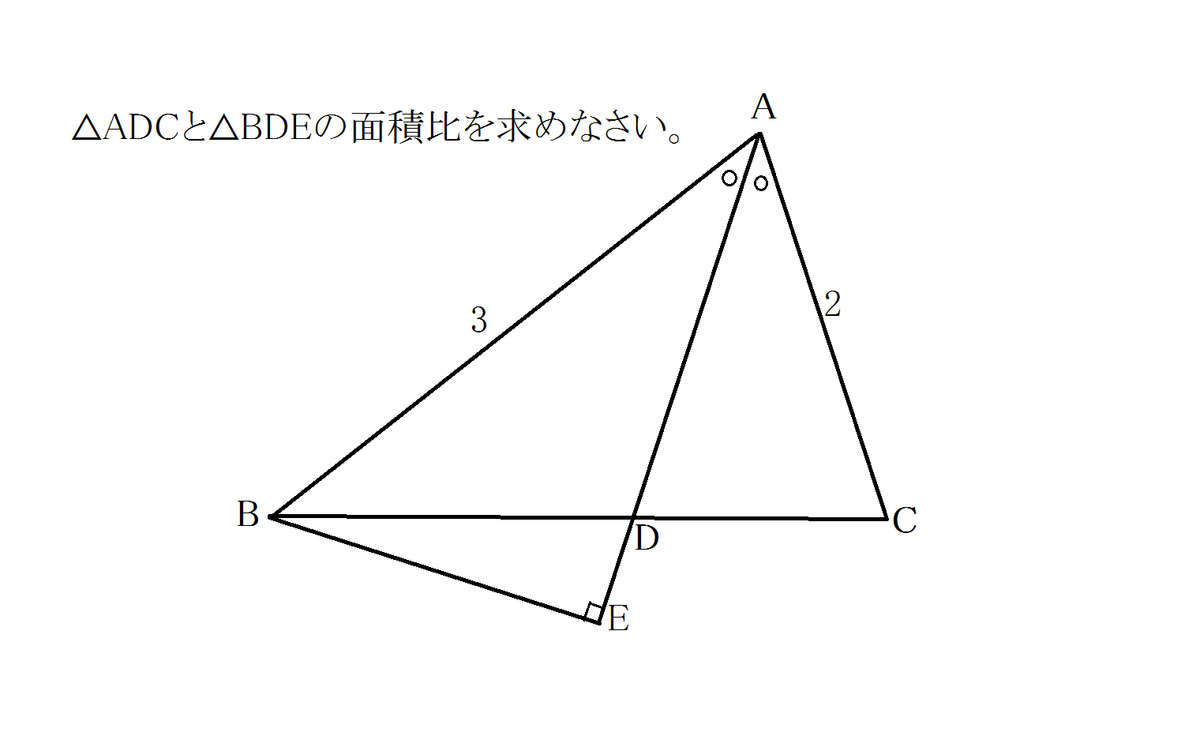



中学数学発展 シンプルだけど難しい ラ サールの難問 平面図形 定期テストや高校入試に レオンの中学数学探検所
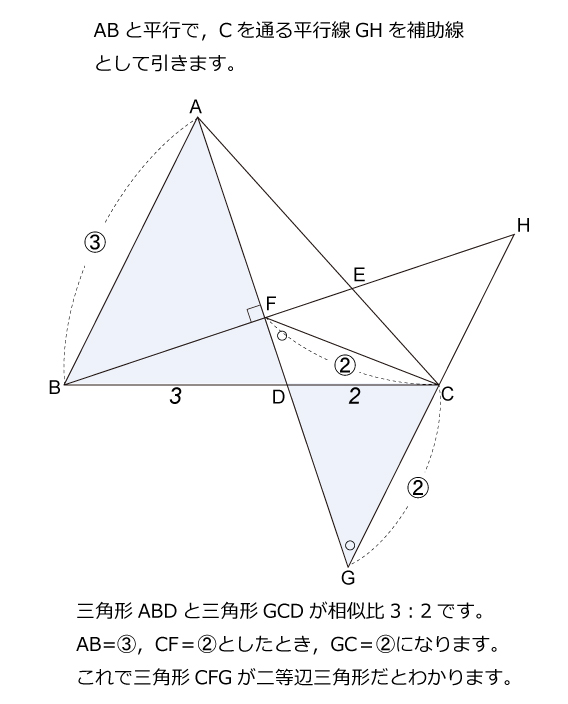



灘中解説速報 16年第10問 平面図形 難問 算数星人のweb問題集 中学受験算数の問題に挑戦



0 件のコメント:
コメントを投稿